The PANEL Procedure

Da Silva Method (Variance-Component Moving Average Model)

The Da Silva method assumes that the observed value of the dependent variable at the tth time point on the ith cross-sectional unit can be expressed as

\[ y_{it}= \mb{x} _{it}^{'}{\beta } + a_{i}+ b_{t}+ e_{it} \hspace{.3 in} i=1, {\ldots }, \mi{N} ;t=1, {\ldots }, \mi{T} \]

where

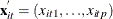${ \mb{x} _{it}^{'}=( x_{it1}, {\ldots }, x_{itp})}$ is a vector of explanatory variables for the tth time point and ith cross-sectional unit

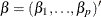${{\beta }=( {\beta }_{1}, {\ldots } , {\beta }_{p}{)’}}$ is the vector of parameters

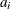${a_{i}}$ is a time-invariant, cross-sectional unit effect

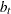${b_{t}}$ is a cross-sectionally invariant time effect

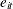${e_{it}}$ is a residual effect unaccounted for by the explanatory variables and the specific time and cross-sectional unit effects

Since the observations are arranged first by cross sections, then by time periods within cross sections, these equations can be written in matrix notation as

\[ \mb{y} =\mb{X} {\beta }+\mb{u} \]

where

\[ \mb{u} =(\mb{a} {\otimes }\mb{1} _{T})+(\mb{1} _{N}{\otimes }\mb{b} )+\mb{e} \]
\[ \mb{y} = (y_{11},{\ldots },y_{1T}, y_{21},{\ldots },y_{NT}{)’} \]
\[ \mb{X} =(\mb{x} _{11},{\ldots },\mb{x} _{1T},\mb{x} _{21},{\ldots } ,\mb{x} _{NT}{)’} \]
\[ \mb{a} =(a_{1}{\ldots }a_{N}{)’} \]
\[ \mb{b} =(b_{1}{\ldots }b_{T}{)’} \]
\[ \mb{e} = (e_{11},{\ldots },e_{1T}, e_{21},{\ldots },e_{NT}{)’} \]

Here 1 $_{N}$ is an ${\mi{N} \times 1}$ vector with all elements equal to 1, and ${\otimes }$ denotes the Kronecker product.

The following conditions are assumed:

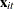  1. ${ \mb{x} _{it}}$ is a sequence of nonstochastic, known 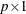${p{\times }1}$ vectors in 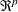${ {\Re }^{p}}$ whose elements are uniformly bounded in 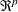${ {\Re }^{p}}$. The matrix X has a full column rank p.

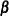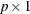  2. $\bbeta $ is a ${p \times 1}$ constant vector of unknown parameters.

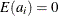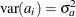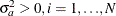  3. a is a vector of uncorrelated random variables such that ${{E}( a_{i})=0}$ and ${\mr{var}( a_{i})= {\sigma }^{2}_{a}}$, ${ {\sigma }^{2}_{a}>0, i=1, {\ldots }, \mi{N} }$.

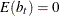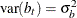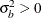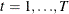  4. b is a vector of uncorrelated random variables such that ${{E}( b_{t})=0}$ and $\mr{var}( b_{t})= {\sigma }^{2}_{b}$ where ${\sigma }^{2}_{b}>0$ and $ t=1, {\ldots }, \mi{T} $.

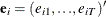  5. ${ \mb{e} _{i}=( e_{i1},{\ldots },e_{iT}{)’}}$ is a sample of a realization of a finite moving-average time series of order 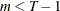${m < \mi{T} -1}$ for each i ; hence,

    \[ e_{it}={\alpha }_{0} {\epsilon }_{it}+ {\alpha }_{1} {\epsilon }_{it-1}+{\ldots }+ {\alpha }_{m} {\epsilon }_{it-m} \; \; \; \; t=1,{\ldots },\mi{T} ; i=1,{\ldots },\mi{N} \]

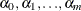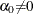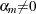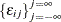    where ${{\alpha }_{0}, {\alpha }_{1},{\ldots }, {\alpha }_{m}}$ are unknown constants such that ${\alpha }_{0}{\ne }0$ and ${{\alpha }_{m}{\ne }0}$, and ${ \{ {\epsilon }_{ij}\} ^{j={\infty }}_{j=-{\infty }}}$ is a white noise process for each i—that is, a sequence of uncorrelated random variables with 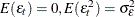${{E}( {\epsilon }_{t})=0,{E}( {\epsilon }^{2}_{t})= {\sigma }^{2}_{{\epsilon }} }$, and ${ {\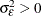sigma }^{2}_{{\epsilon }}>0 }$. 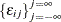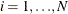${ \{ {\epsilon }_{ij}\} ^{j={\infty }}_{j=-{\infty }}}$ for ${i=1, {\ldots }, \mi{N} }$ are mutually uncorrelated.

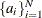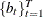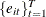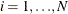  6. The sets of random variables ${ \{ a_{i}\} ^{N}_{i=1}}$, ${ \{ b_{t}\} ^{T}_{t=1}}$, and ${ \{ e_{it}\} ^{T}_{t=1}}$ for ${i=1, {\ldots }, \mi{N} }$ are mutually uncorrelated.

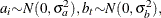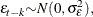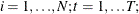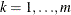  7. The random terms have normal distributions ${ a_{i}{\sim }{N}(0, {\sigma }^{2}_{a}), b_{t}{\sim }{N}(0, {\sigma }^{2}_{b}), }$ and ${ {\epsilon }_{t-k}{\sim }{N}(0, {\sigma }^{2}_{{\epsilon }}), }$ for ${i=1, {\ldots }, \mi{N} ; t=1,{\ldots } \mi{T} ;} $ and $k=1, {\ldots }, m$.

If assumptions 1–6 are satisfied, then

\[ {E}(\mb{y} )=\mb{X} {\beta } \]

and

\[ \mr{var}(\mb{y} )= {\sigma }^{2}_{a} (I_{N}{\otimes }J_{T})+ {\sigma }^{2}_{b}(J_{N}{\otimes }I_{T})+ (I_{N}{\otimes }{\Psi }_{T}) \]

where ${{\Psi }_{T}}$ is a ${\mi{T} \times \mi{T} }$ matrix with elements ${{\psi }_{ts}}$ as follows:

\[ \mr{Cov}( e_{it} e_{is})= \begin{cases} {\psi }({|t-s|}) & \mr{if}\hspace{.1 in} {|t-s|} {\le } m \\ 0 & \mr{if} \hspace{.1 in}{|t-s|} > m \end{cases} \]

where ${{\psi }(k) = {\sigma }^{2}_{{\epsilon }}\sum _{j=0}^{m-k}{{\alpha }_{j}{\alpha }_{j+k}}}$ for ${k={|t-s|}}$. For the definition of ${I_{N}}$, ${I_{T}}$, ${J_{N}}$, and ${J_{T}}$, see the section Fuller and Battese’s Method.

The covariance matrix, denoted by V, can be written in the form

\[ \mb{V} = {\sigma }^{2}_{a}(I_{N}{\otimes }J_{T}) + {\sigma }^{2}_{b}(J_{N}{\otimes }I_{T}) +\sum _{k=0}^{m}{{\psi }(k)(I_{N}{\otimes } {\Psi }^{(k)}_{T})} \]

where ${ {\Psi }^{(0)}_{T}=I_{T}}$, and, for k =1,${\ldots }$, m, ${ {\Psi }^{(k)}_{T}}$ is a band matrix whose kth off-diagonal elements are 1’s and all other elements are 0’s.

Thus, the covariance matrix of the vector of observations y has the form

\[ {\mr{Var}}(\mb{y} )=\sum _{k=1}^{m+3}{{\nu }_{k}V_{k}} \]

where

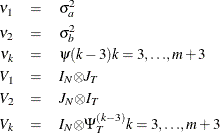
\begin{eqnarray*} {\nu }_{1}& =& {\sigma }^{2}_{a} \\ {\nu }_{2}& =& {\sigma }^{2}_{b} \\ {\nu }_{k}& =& {\psi }(k-3) k=3,{\ldots }, m+3 \\ V_{1}& =& I_{N}{\otimes }J_{T} \\ V_{2}& =& J_{N}{\otimes }I_{T} \\ V_{k}& =& I_{N}{\otimes } {\Psi }^{(k-3)}_{T} k=3,{\ldots }, m+3 \nonumber \end{eqnarray*}

The estimator of $\bbeta $ is a two-step GLS-type estimator—that is, GLS with the unknown covariance matrix replaced by a suitable estimator of V. It is obtained by substituting Seely estimates for the scalar multiples ${{\nu }_{k},k=1, 2, {\ldots }, m+3}$.

Seely (1969) presents a general theory of unbiased estimation when the choice of estimators is restricted to finite dimensional vector spaces, with a special emphasis on quadratic estimation of functions of the form ${\sum _{i=1}^{n}{{\delta }_{i}{\nu }_{i}}}$.

The parameters ${{\nu }_{i}}$ (i =1,${\ldots }$, n) are associated with a linear model E(y )=X ${\beta }$ with covariance matrix ${\sum _{i=1}^{n}{{\nu }_{i}V_{i}}}$ where ${V_{i}}$ (i =1, ${\ldots }$, n) are real symmetric matrices. The method is also discussed by Seely (1970b, 1970a); Seely and Zyskind (1971). Seely and Soong (1971) consider the MINQUE principle, using an approach along the lines of Seely (1969).