The HPSEVERITY Procedure

SCALEMODEL Statement

SCALEMODEL regressor-variable-list </ scalemodel-options> ;

The SCALEMODEL statement specifies regression variables. All the variables that you specify in this statement must be present in the input data set that you specify by using the DATA= option in the PROC HPSEVERITY statement. The scale parameter of each candidate distribution is linked to a linear combination of these regression variables along with an intercept. If a distribution does not have a scale parameter, then a model based on that distribution is not estimated. If you specify more than one SCALEMODEL statement, then the first statement is used.

The regressor variables are expected to have nonmissing values. If any of the variables has a missing value in an observation, then a warning is written to the SAS log and that observation is ignored.

For more information about modeling regression effects, see the section Estimating Regression Effects.

You can specify the following scalemodel-options in the SCALEMODEL statement:

DFMIXTURE=method-name <(method-options)>

specifies the method for computing representative estimates of the cumulative distribution function (CDF).

When you specify regression variables, the scale of the distribution depends on the values of the regressors. For a given distribution family, each observation in the input data set implies a different scaled version of the distribution. To compute estimates of CDF that are comparable across different distribution families, PROC HPSEVERITY needs to construct a single representative distribution from all such distributions. You can specify one of the following method-name values to specify the method that is used to construct the representative distribution. For more information about each of the methods, see the section CDF Estimates with Regression Effects.

FULL

specifies that the representative distribution be the mixture of 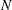$N$ distributions such that each distribution has a scale value that is implied by each of the 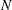$N$ observations that are used for estimation. This method is the slowest.

MEAN

specifies that the representative distribution be the one-point mixture of the distribution whose scale value is the mean of the 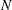$N$ scale values that are implied by the 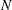$N$ observations that are used for estimation. If you do not specify the DFMIXTURE= option, then this method is used by default. This is also the fastest method.

QUANTILE <(K=q)>

specifies that the representative distribution be the mixture of a fixed number of distributions whose scale values are the quantiles from the sample of 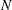$N$ scale values that are implied by the 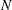$N$ observations in the current BY group (or in the entire DATA= data set if you do not specify the BY statement).

You can use the K= option to specify the number of distributions in the mixture. If you specify K=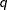 $\Argument{q}$ , then the mixture contains 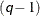$(\Argument{q}-1)$ distributions such that each distribution has as its scale one of the 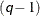$(\Argument{q}-1)$ -quantiles.

If you do not specify the K= option, then PROC HPSEVERITY uses the default of 2, which implies the use of a one-point mixture with a distribution whose scale value is the median of all scale values.

RANDOM <(random-method-options)>

specifies that the representative distribution be the mixture of a fixed number of distributions whose scale values are the scale values that are implied by a randomly chosen subset of the set of all observations in the current BY group (or in the entire DATA= data set if you do not specify the BY statement). The same subset of observations is used for each distribution family.

You can specify the following random-method-options to specify how the subset is chosen:

K=r: specifies the number of distributions to include in the mixture. If you do not specify this option, then PROC HPSEVERITY uses the default of 15.
SEED=number: specifies the seed that is used to generate the uniform random sample of observation indices. If you do not specify this option, then PROC HPSEVERITY generates a seed internally that is based on the current value of the system clock.

OFFSET=offset-variable-name

specifies the name of the offset variable in the scale regression model. An offset variable is a regressor variable whose regression coefficient is known to be 1. For more information, see the section Offset Variable.