The HPSEVERITY Procedure

Details of Optimization Algorithms

Subsections:

Overview
Choosing an Optimization Algorithm

Overview

There are several optimization techniques available. You can choose a particular optimizer with the TECH=name option in the PROC statement or NLOPTIONS statement.

Table 9.4: Optimization Techniques

Algorithm	TECH=
Trust region Method	TRUREG
Newton-Raphson method with line search	NEWRAP
Newton-Raphson method with ridging	NRRIDG
Quasi-Newton methods (DBFGS, DDFP, BFGS, DFP)	QUANEW
Double-dogleg method (DBFGS, DDFP)	DBLDOG
Conjugate gradient methods (PB, FR, PR, CD)	CONGRA
Nelder-Mead simplex method	NMSIMP

No algorithm for optimizing general nonlinear functions exists that always finds the global optimum for a general nonlinear minimization problem in a reasonable amount of time. Since no single optimization technique is invariably superior to others, NLO provides a variety of optimization techniques that work well in various circumstances. However, you can devise problems for which none of the techniques in NLO can find the correct solution. Moreover, nonlinear optimization can be computationally expensive in terms of time and memory, so you must be careful when matching an algorithm to a problem.

All optimization techniques in NLO use $O(n^2)$ memory except the conjugate gradient methods, which use only $O(n)$ of memory and are designed to optimize problems with many parameters. These iterative techniques require repeated computation of the following:

the function value (optimization criterion)
the gradient vector (first-order partial derivatives)
for some techniques, the (approximate) Hessian matrix (second-order partial derivatives)

However, since each of the optimizers requires different derivatives, some computational efficiencies can be gained. Table 9.5 shows which derivatives are required for each optimization technique. (FOD means that first-order derivatives or the gradient is computed; SOD means that second-order derivatives or the Hessian is computed.)

Table 9.5: Optimization Computations

Algorithm	FOD	SOD
TRUREG	x	x
NEWRAP	x	x
NRRIDG	x	x
QUANEW	x	-
DBLDOG	x	-
CONGRA	x	-
NMSIMP	-	-

Each optimization method uses one or more convergence criteria that determine when it has converged. The various termination criteria are listed and described in the previous section. An algorithm is considered to have converged when any one of the convergence criteria is satisfied. For example, under the default settings, the QUANEW algorithm converges if ABSGCONV $<$ 1E–5, FCONV $< 10^{-\mbox{FDIGITS}}$ , or GCONV $<$ 1E–8.

Choosing an Optimization Algorithm

The factors for choosing a particular optimization technique for a particular problem are complex and might involve trial and error.

For many optimization problems, computing the gradient takes more computer time than computing the function value, and computing the Hessian sometimes takes much more computer time and memory than computing the gradient, especially when there are many decision variables. Unfortunately, optimization techniques that do not use some kind of Hessian approximation usually require many more iterations than techniques that do use a Hessian matrix. As a result the total run time of these techniques is often longer. Techniques that do not use the Hessian also tend to be less reliable. For example, they can more easily terminate at stationary points rather than at global optima.

A few general remarks about the various optimization techniques follow:

The second-derivative methods TRUREG, NEWRAP, and NRRIDG are best for small problems where the Hessian matrix is not expensive to compute. Sometimes the NRRIDG algorithm can be faster than the TRUREG algorithm, but TRUREG can be more stable. The NRRIDG algorithm requires only one matrix with 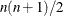$n(n+1)/2$ double words; TRUREG and NEWRAP require two such matrices.
The first-derivative methods QUANEW and DBLDOG are best for medium-sized problems where the objective function and the gradient are much faster to evaluate than the Hessian. The QUANEW and DBLDOG algorithms generally require more iterations than TRUREG, NRRIDG, and NEWRAP, but each iteration can be much faster. The QUANEW and DBLDOG algorithms require only the gradient to update an approximate Hessian, and they require slightly less memory than TRUREG or NEWRAP (essentially one matrix with 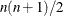$n(n+1)/2$ double words). QUANEW is the default optimization method.
The first-derivative method CONGRA is best for large problems where the objective function and the gradient can be computed much faster than the Hessian and where too much memory is required to store the (approximate) Hessian. The CONGRA algorithm generally requires more iterations than QUANEW or DBLDOG, but each iteration can be much faster. Since CONGRA requires only a factor of $n$ double-word memory, many large applications can be solved only by CONGRA.
The no-derivative method NMSIMP is best for small problems where derivatives are not continuous or are very difficult to compute.