-
ABSCONV=r
ABSTOL=r
-
specifies an absolute function value convergence criterion. For minimization, termination requires 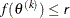 . The default value of r is the negative square root of the largest double-precision value, which serves only as a protection against overflows.
. The default value of r is the negative square root of the largest double-precision value, which serves only as a protection against overflows.
-
ABSFCONV=r
ABSFTOL=r
-
specifies an absolute function difference convergence criterion. For all techniques except NMSIMP, termination requires a
small change of the function value in successive iterations:
The same formula is used for the NMSIMP technique, but 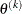 is defined as the vertex with the lowest function value, and
is defined as the vertex with the lowest function value, and 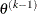 is defined as the vertex with the highest function value in the simplex. The default value is
is defined as the vertex with the highest function value in the simplex. The default value is 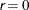 .
.
-
ABSGCONV=r
ABSGTOL=r
-
specifies an absolute gradient convergence criterion. Termination requires the maximum absolute gradient element to be small:
This criterion is not used by the NMSIMP technique. The default value is r=1E–5.
-
ABSXCONV=r
ABSXTOL=r
-
specifies an absolute parameter convergence criterion. For all techniques except NMSIMP, termination requires a small Euclidean
distance between successive parameter vectors,
For the NMSIMP technique, termination requires either a small length 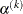 of the vertices of a restart simplex,
of the vertices of a restart simplex,
or a small simplex size,
where the simplex size 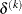 is defined as the L1 distance from the simplex vertex
is defined as the L1 distance from the simplex vertex 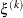 with the smallest function value to the other simplex points
with the smallest function value to the other simplex points 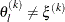 :
:
The default is r=1E–8 for the NMSIMP technique and 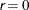 otherwise.
otherwise.
-
FCONV=r
FTOL=r
-
specifies a relative function convergence criterion. For all techniques except NMSIMP, termination requires a small relative
change of the function value in successive iterations,
where FSIZE is defined by the FSIZE= option. The same formula is used for the NMSIMP technique, but 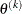 is defined as the vertex with the lowest function value, and
is defined as the vertex with the lowest function value, and 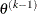 is defined as the vertex with the highest function value in the simplex.
is defined as the vertex with the highest function value in the simplex.
The default value is 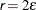 , where
, where  denotes the machine precision constant, which is the smallest double-precision floating-point number such that
denotes the machine precision constant, which is the smallest double-precision floating-point number such that 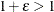 .
.
-
FCONV2=r
FTOL2=r
-
specifies another function convergence criterion.
For all techniques except NMSIMP, termination requires a small predicted reduction of the objective function:
The predicted reduction
is computed by approximating the objective function 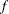 by the first two terms of the Taylor series and substituting the Newton step
by the first two terms of the Taylor series and substituting the Newton step
For the NMSIMP technique, termination requires a small standard deviation of the function values of the 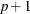 simplex vertices
simplex vertices 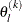 ,
, 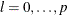 ,
, ![$ \sqrt { \frac{1}{p+1} \sum _ l \left[ f(\theta _ l^{(k)}) - \overline{f}(\theta ^{(k)}) \right]^2 } \leq \Argument{r} $](images/etshpug_hpseverity0068.png) where
where 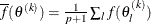 . If there are
. If there are 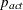 boundary constraints active at
boundary constraints active at 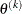 , the mean and standard deviation are computed only for the
, the mean and standard deviation are computed only for the 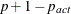 unconstrained vertices.
unconstrained vertices.
The default value is r=1E–6 for the NMSIMP technique and 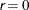 otherwise.
otherwise.
-
FSIZE=r
-
specifies the FSIZE parameter of the relative function and relative gradient termination criteria. The default value is r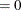 . For more information, see the FCONV= and GCONV= options.
. For more information, see the FCONV= and GCONV= options.
-
GCONV=r
GTOL=r
-
specifies a relative gradient convergence criterion. For all techniques except CONGRA and NMSIMP, termination requires that
the normalized predicted function reduction is small,
where FSIZE is defined by the FSIZE= option. For the CONGRA technique (where a reliable Hessian estimate 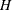 is not available), the following criterion is used:
is not available), the following criterion is used:
This criterion is not used by the NMSIMP technique. The default value is 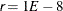 .
.
-
MAXFUNC=i
MAXFU=i
-
specifies the maximum number i of function calls in the optimization process. The default values are
Note that the optimization can terminate only after completing a full iteration. Therefore, the number of function calls
that is actually performed can exceed the number that you specify by the MAXFUNC= option.
-
MAXITER=i
MAXIT=i
-
specifies the maximum number i of iterations in the optimization process. The default values are
These default values are also valid when you specify a missing value for i.
-
MAXTIME=r
-
specifies an upper limit of r seconds of CPU time for the optimization process. The default value is the largest floating-point double representation of
your computer. The time that you specify in the MAXTIME= option is checked only once at the end of each iteration. Therefore,
the actual running time can be much longer than that you specify by the MAXTIME= option. The actual running time includes
the rest of the time needed to finish the iteration and the time needed to generate the output of the results.
-
MINITER=i
MINIT=i
-
specifies the minimum number of iterations. The default value is 0. If you request more iterations than are actually needed
for convergence to a stationary point, the optimization algorithms can behave strangely. For example, the effect of rounding
errors can prevent the algorithm from continuing for the required number of iterations.
-
TECHNIQUE=name
TECH=name
-
specifies the optimization technique. Valid values for name are as follows:
- CONGRA
-
performs a conjugate-gradient optimization.
- DBLDOG
-
performs a version of double-dogleg optimization.
- NMSIMP
-
performs a Nelder-Mead simplex optimization.
- NONE
-
does not perform any optimization. This option can be used as follows:
- NEWRAP
-
performs a Newton-Raphson optimization that combines a line-search algorithm with ridging.
- NRRIDG
-
performs a Newton-Raphson optimization with ridging.
- QUANEW
-
performs a quasi-Newton optimization.
- TRUREG
-
performs a trust region optimization. This is the default estimation method.
For more information about optimization algorithms, see the section Details of Optimization Algorithms.
-
XCONV=r
XTOL=r
-
specifies the relative parameter convergence criterion. For all techniques except NMSIMP, termination requires a small relative
parameter change in subsequent iterations:
For the NMSIMP technique, the same formula is used, but 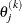 is defined as the vertex that has the lowest function value and
is defined as the vertex that has the lowest function value and 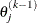 is defined as the vertex that has the highest function value in the simplex. The default value is r=1E–8 for the NMSIMP technique and
is defined as the vertex that has the highest function value in the simplex. The default value is r=1E–8 for the NMSIMP technique and 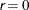 otherwise.
otherwise.
-
XSIZE=r
-
specifies the XSIZE parameter of the relative parameter termination criterion. The value of r must be greater than or equal to 0; the default is 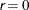 . For more information, see the XCONV= option.
. For more information, see the XCONV= option.


 Predefined DistributionsCensoring and TruncationParameter Estimation MethodDetails of Optimization AlgorithmsParameter InitializationEstimating Regression EffectsEmpirical Distribution Function Estimation MethodsStatistics of FitDistributed and Multithreaded ComputationDefining a Severity Distribution Model with the FCMP ProcedurePredefined Utility FunctionsScoring FunctionsCustom Objective FunctionsInput Data SetsOutput Data SetsDisplayed Output
Predefined DistributionsCensoring and TruncationParameter Estimation MethodDetails of Optimization AlgorithmsParameter InitializationEstimating Regression EffectsEmpirical Distribution Function Estimation MethodsStatistics of FitDistributed and Multithreaded ComputationDefining a Severity Distribution Model with the FCMP ProcedurePredefined Utility FunctionsScoring FunctionsCustom Objective FunctionsInput Data SetsOutput Data SetsDisplayed Output Defining a Model for Gaussian DistributionDefining a Model for the Gaussian Distribution with a Scale ParameterDefining a Model for Mixed-Tail DistributionsFitting a Scaled Tweedie Model with RegressorsFitting Distributions to Interval-Censored DataBenefits of Distributed and Multithreaded ComputingEstimating Parameters Using Cramér-von Mises EstimatorDefining a Finite Mixture Model That Has a Scale ParameterPredicting Mean and Value-at-Risk by Using Scoring Functions
Defining a Model for Gaussian DistributionDefining a Model for the Gaussian Distribution with a Scale ParameterDefining a Model for Mixed-Tail DistributionsFitting a Scaled Tweedie Model with RegressorsFitting Distributions to Interval-Censored DataBenefits of Distributed and Multithreaded ComputingEstimating Parameters Using Cramér-von Mises EstimatorDefining a Finite Mixture Model That Has a Scale ParameterPredicting Mean and Value-at-Risk by Using Scoring Functions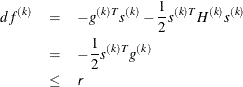
![\[ \frac{\max _ j |\theta _ j^{(k)} - \theta _ j^{(k-1)}|}{\max (|\theta _ j^{(k)}|,|\theta _ j^{(k-1)}|,\mbox{XSIZE})} \leq \Argument{r} \]](images/etshpug_hpseverity0077.png)