The HPSEVERITY Procedure

Distributed and Multithreaded Computation

Subsections:

Distributed Computing
Multithreading
Combining the Power of Distributed and Multithreading Computing

PROC HPSEVERITY makes an attempt to use all the computational resources that you specify in the PERFORMANCE statement in order to complete the assigned tasks as fast as possible. This section describes the distributed and multithreading computing methods that PROC HPSEVERITY uses.

Distributed Computing

Distributed computing refers to the organization of computation work into multiple tasks that are processed on different nodes; a node is one of the machines that constitute the grid. The number of nodes that PROC HPSEVERITY uses is determined by the distributed processing execution mode. If you specify the client-data (or local-data) mode of execution, then the number of nodes is determined by the NODES= option in the PERFORMANCE statement. If you are using the alongside-the-database mode of execution, then PROC HPSEVERITY determines the number of nodes internally by using the information that is associated with the DATA= data set and the grid information that you specify either in the PERFORMANCE statement or in the grid environment variables. For more information about distributed processing modes, see the section Processing Modes.

In the client-data model, PROC HPSEVERITY distributes the input data across the number of nodes that you specify by sending the first observation to the first node, the second observation to the second node, and so on.

In the alongside-the-database model, PROC HPSEVERITY uses the existing distributed organization of the data. You do not need to specify the NODES= option.

The number of nodes that are used for distributed computing is displayed in the “Performance Information” table, which is part of the default output.

Multithreading

Threading refers to the organization of computational work into multiple tasks (processing units that can be scheduled by the operating system). A task is associated with a thread. Multithreading refers to the concurrent execution of threads. When multithreading is possible, you can achieve more substantial performance gains than you can with sequential (single-threaded) execution.

The number of threads the HPSEVERITY procedure spawns is determined by the number of CPUs on a machine. You can control the number of CPUs in the following ways:

You can use the CPUCOUNT= SAS system option to specify the CPU count. For example, if you specify the following statement, then PROC HPSEVERITY schedules threads as if it were executing on a system that had four CPUs, regardless of the actual CPU count:
```
options cpucount=4;
```
You can use this specification only in single-machine mode, and it does not take effect if the THREADS system option is turned off.

The default value of the CPUCOUNT= system option might not equal the number of all the logical CPU cores available on your machine, such as those available because of hyperthreading. To allow PROC HPSEVERITY to use all the logical cores in single-machine mode, specify the following OPTIONS statement:
```
options cpucount=actual;
```
You can specify the NTHREADS= option in the PERFORMANCE statement. This specification overrides the THREADS and CPUCOUNT= system options. Specify NTHREADS=1 to force single-threaded execution.

If you do not specify the NTHREADS= option and the THREADS system option is turned on, then the number of threads that are used in distributed mode is equal to the total number of logical CPU cores available on each node of the grid, and the number of threads used in single-machine mode is determined by the CPUCOUNT= system option.

If you do not specify the NTHREADS= option and the THREADS system option is turned off, then only one thread of execution is used in both single-machine and distributed modes.

The number of threads per machine is displayed in the “Performance Information” table, which is part of the default output.

Performance improvement is not always guaranteed when you use more threads, for several reasons: the increased cost of communication and synchronization among threads might offset the reduced cost of computation, the hyperthreading feature of the processor might not be very efficient for floating-point computations, and other applications might be running on the machine.

Combining the Power of Distributed and Multithreading Computing

The HPSEVERITY procedure combines the powers of distributed and multithreading paradigms by using a data-parallel model. In particular, the distributed tasks are defined by dividing the data among multiple nodes, and within one node, the multithreading tasks are defined by further dividing the local data among the threads. For example, if the input data set has 10,000 observations and you are running on a grid that has five nodes, then each node processes 2,000 observations (this assumes that if you specify an alongside-the-database model, then you have equally and randomly divided the input data among the nodes). Further, if each node has eight CPUs, then 250 observations are associated with each thread within the node. All computations that require access to the data are then distributed and multithreaded.

Note that in single-machine mode (see the section Processing Modes), only multithreading is available.

When you specify more than one candidate distribution model, for some tasks PROC HPSEVERITY exploits the independence among models by processing multiple models in parallel on a single node such that each model is assigned to one of the threads executing in parallel. When a thread finishes processing the assigned model, it starts processing the next unprocessed model, if one exists.

The computations that take advantage of the distributed and multithreaded model include the following:

Validation and preparation of data: In this stage, the observations in the input data set are validated and transformed, if necessary. The summary statistics of the data are prepared. Because each observation is independent, the computations can be distributed among nodes and among threads within nodes without significant communication overhead.
Initialization of distribution parameters: In this stage, the parallelism is achieved by initializing multiple models in parallel. The only computational step that is not fully parallelized in this release is the step of computing empirical distribution function (EDF) estimates, which are required when PROC HPSEVERITY needs to invoke a distribution’s PARMINIT subroutine to initialize distribution parameters. The EDF estimation step is not amenable to full-fledged parallelism because it requires sequential access to sorted data, especially when the loss variable is modified by truncation effects. When the data are distributed across nodes, the EDF computations take place on local data and the PARMINIT function is invoked on the local data by using the local EDF estimates. The initial values that are supplied to the nonlinear optimizer are computed by averaging the local estimates of the distribution parameters that are returned by the PARMINIT functions on each node.
Initialization of regression parameters (if you specify the SCALEMODEL statement): In this stage, if you do not specify initial values for the regression parameters by using the INEST= data set, then PROC HPSEVERITY initializes those parameters by solving a linear regression problem 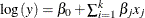$\log {(y)} = \beta _0 + \sum _{i=1}^{k} \beta _ j x_ j$ . For more information, see the section Parameter Initialization for Regression Models. The most computationally intensive step is the formation of the crossproducts matrix. PROC HPSEVERITY exploits the parallelism by observing the fact that the contribution to the crossproducts matrix due to one observation is independent from the contribution due to another observation. Each node computes the contribution of its local data to each entry of the crossproducts matrix. Within each node, each thread computes the contribution of its chunk of data to each entry of the crossproducts matrix. On each node, the contributions from all the threads are added up to form the contribution due to all of the local data. The partial crossproducts matrices are then gathered from all nodes on a central node, which sums them up to form the final crossproducts matrix.
Optimization: In this stage, the nonlinear optimizer iterates over the parameter space in search of the optimal set of parameters. In each iteration, it evaluates the objective function along with the gradient and Hessian of the objective function, if needed by the optimization method. Within one iteration, for the current estimates of the parameters, each observation’s contribution to the objective function, gradient, and Hessian is independent of another observation. This enables PROC HPSEVERITY to fully exploit the distributed and multithreaded paradigms to efficiently parallelize each iteration of the algorithm.