The GAMPL Procedure

PROC GAMPL Statement

Subsections:

  • PROC GAMPL <options>;

The PROC GAMPL statement invokes the procedure. Table 42.1 summarizes the available options in the PROC GAMPL statement by function. The options are then described fully in alphabetical order.

Table 42.1: PROC GAMPL Statement Options

Option

Description

Basic Options

ALPHA=

Specifies a global significance level

DATA=

Specifies the input data set

NAMELEN=

Limits the length of effect names

SEED=

Sets the seed for pseudorandom number generation

Display Options

ITDETAILS

Displays the "Iteration History" table

NOCLPRINT

Limits or suppresses the display of classification variable levels

NOPRINT

Suppresses ODS output

PLOTS=

Controls plots that are produced through ODS Graphics

Optimization Subject Options

PLIKEOPTIONS

Sets optimization parameters for likelihood estimation

SMOOTHOPTIONS

Sets optimization parameters for smoothing parameter estimation

Tolerance Options

SINGCHOL=

Tunes the singularity criterion for Cholesky decompositions

SINGSWEEP=

Tunes the singularity criterion for the sweep operator

SINGULAR=

Tunes the general singularity criterion

User-Defined Format Options

FMTLIBXML=

Specifies the file reference for a format stream


You can specify the following options in the PROC GAMPL statement.

ALPHA=number

specifies a global significance level for the hypothesis testing of smoothing components and the construction of Bayesian confidence bands of predictions. The confidence level is 1 – number. The value of number must be between 0 and 1; the default is 0.05. You can override this global significance level for Bayesian confidence bands of predictions by specifying the ALPHA= option in the OUTPUT statement.

DATA=SAS-data-set

names the input SAS data set for PROC GAMPL to use. The default is the most recently created data set.

If the procedure executes in distributed mode, the input data are distributed to memory on the appliance nodes and analyzed in parallel, unless the data are already distributed in the appliance database. In that case, PROC GAMPL reads the data alongside the distributed database. For information about the various execution modes, see the section Processing Modes in SAS/STAT 14.1 User's Guide: High-Performance Procedures. For information about the alongside-the-database model, see the section Alongside-the-Database Execution in SAS/STAT 14.1 User's Guide: High-Performance Procedures.

FMTLIBXML=file-ref

specifies the file reference for the XML stream that contains user-defined format definitions. User-defined formats are handled differently in a distributed computing environment than they are in other SAS products. For information about how to generate an XML stream for your formats, see the section Working with Formats in SAS/STAT 14.1 User's Guide: High-Performance Procedures.

ITDETAILS

adds to the "Iteration History" table the current values of the parameter estimates and their gradients. If the optimization algorithm is used to determine at least one smoothing parameter, the table lists values for smoothing parameters. If all smoothing parameters are fixed or a parametric generalized linear model is specified, the table lists values for regression parameters. These quantities are reported only for parameters that participate in the optimization.

NAMELEN=number

specifies the length to which long effect names are shortened. The value of number must be an integer greater than or equal to 20. By default, NAMELEN=20.

NOCLPRINT<=number>

suppresses the display of the "Class Level Information" table if you do not specify number. If you specify number, the values of the classification variables are displayed for only those variables whose number of levels is less than number. Specifying a number helps reduce the size of the "Class Level Information" table if some classification variables have a large number of levels.

NOPRINT

suppresses the generation of ODS output.

PLIKEOPTIONS(optimization-parameters)

sets optimization parameters for either maximum or penalized likelihood estimation. For more information about how to specify optimization-parameters, see the section Optimization Parameters.

PLOTS <(global-plot-option)> <= plot-requests <(option)>>

controls the plots that are produced through ODS Graphics. When ODS Graphics is enabled, PROC GAMPL produces by default a panel of plots of partial prediction curves or surfaces of smoothing components.

ODS Graphics must be enabled before plots can be requested. For example: 

ods graphics on;

proc gampl plots;
   model y=spline(x1) spline(x2);
run;

ods graphics off;

For more information about enabling and disabling ODS Graphics, see the section Enabling and Disabling ODS Graphics in Chapter 21: Statistical Graphics Using ODS.

You can specify the following global-plot-option, which applies to the smoothing component plots that the GAMPL procedure generates:

UNPACK |UNPACKPANEL

suppresses paneling. By default, multiple smoothing component plots can appear in some output panels. Specify UNPACK to get each plot individually.

You can specify the following plot-requests:

ALL

requests that all default plots be produced.

COMPONENTS <(component-option)>

plots a panel of smoothing components of the fitted model. You can specify the following component-option:

COMMONAXES

requests that the smoothing component plots use a common vertical axis except for bivariate contour plots. This option enables you to visually judge the relative effect size.

NONE

suppresses all plots.

SEED=number

specifies an integer that is used to start the pseudorandom number generator for subset sampling from observations to form knots if necessary and for truncated eigendecomposition. If you do not specify this option, or if number$~ \le $ 0, the seed is generated from the time of day, which is read from the computer’s clock.

SINGCHOL=number

tunes the singularity criterion in Cholesky decompositions. The default is 1E4 times the machine epsilon; this product is approximately 1E–12 on most computers.

SINGSWEEP=number

tunes the singularity criterion in sweep operations that determine collinearity between spline basis expansions. The default is 1E–8.

SINGULAR=number

tunes the general singularity criterion that is applied in sweep and inversion operations. The default is 1E4 times the machine epsilon; this product is approximately 1E–12 on most computers.

SMOOTHOPTIONS(optimization-parameters)

specifies optimization parameters for smoothing parameter estimation. For more information about how to specify optimization-parameters, see the section Optimization Parameters.

Optimization Parameters

You can specify optimization-parameters for both the PLIKEOPTIONS and SMOOTHOPTIONS options. Depending on the modeling context, some optimization parameters might have no effect. For parametric generalized linear models or generalized additive models that have fixed smoothing parameters, any optimization parameters that you specify in the SMOOTHOPTIONS option are ignored. For the performance iteration method , only the ABSFCONV= , FCONV= , and MAXITER= options are effective for PLIKEOPTIONS . The optimization algorithm is considered to have converged when any one of the convergence criteria that are specified in optimization-parameters is satisfied. Table 42.2 lists the available optimization parameters for both the PLIKEOPTIONS and SMOOTHOPTIONS options.

Table 42.2: Optimization Parameters

Option

Description

ABSCONV=

Tunes the absolute function convergence criterion

ABSFCONV=

Tunes the absolute function difference convergence criterion

ABSGCONV=

Tunes the absolute gradient convergence criterion

FCONV=

Tunes the relative function difference convergence criterion

GCONV=

Tunes the relative gradient convergence criterion

MAXFUNC=

Specifies the maximum number of function evaluations in any optimization

MAXITER=

Chooses the maximum number of iterations in any optimization

MAXTIME=

Specifies the upper limit of CPU time (in seconds) for any optimization

MINITER=

Specifies the minimum number of iterations in any optimization

TECHNIQUE=

Selects the optimization technique


You can specify the following optimization-parameters:

ABSCONV=r
ABSTOL=r

specifies an absolute function convergence criterion. For minimization, termination requires $f(\bpsi ^{(k)}) \leq $ r, where $\bpsi $ is the vector of parameters in the optimization and $f(\cdot )$ is the objective function. The default value of r is the negative square root of the largest double-precision value, which serves only as a protection against overflow.

ABSFCONV=r <n>
ABSFTOL=r <n>

specifies an absolute function difference convergence criterion. For all techniques except NMSIMP, termination requires a small change of the function value in successive iterations,

\[ |f(\bpsi ^{(k-1)}) - f(\bpsi ^{(k)})| \leq r \]

where $\bpsi $ denotes the vector of parameters that participate in the optimization and $f(\cdot )$ is the objective function. The same formula is used for the NMSIMP technique, but $\bpsi {(k)}$ is defined as the vertex that has the lowest function value and $\bpsi ^{(k-1)}$ is defined as the vertex that has the highest function value in the simplex. The optional integer value n specifies the number of successive iterations for which the criterion must be satisfied before the process terminates. By default, ABSFCONV=0.

ABSGCONV=r <n>
ABSGTOL=r <n>

specifies an absolute gradient convergence criterion. Termination requires the maximum absolute gradient element to be small,

\[ \max _ j |g_ j(\bpsi ^{(k)})| \leq r \]

where $\bpsi $ denotes the vector of parameters that participate in the optimization and $g_ j(\cdot )$ is the gradient of the objective function with respect to the jth parameter. This criterion is not used by the NMSIMP technique. The default value is r = 1E–8. The optional integer value n specifies the number of successive iterations for which the criterion must be satisfied before the process terminates.

FCONV=r <n>
FTOL=r <n>

specifies a relative function difference convergence criterion. For all techniques except NMSIMP, termination requires a small relative change of the function value in successive iterations,

\[ \frac{|f(\bpsi ^{(k)}) - f(\bpsi ^{(k-1)})|}{|f(\bpsi ^{(k-1)})|} \leq r \]

where $\bpsi $ denotes the vector of parameters that participate in the optimization and $f(\cdot )$ is the objective function. The same formula is used for the NMSIMP technique, but $\bpsi ^{(k)}$ is defined as the vertex that has the lowest function value and $\bpsi ^{(k-1)}$ is defined as the vertex that has the highest function value in the simplex.

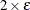
The default value is r = $2\times \epsilon $, where $\epsilon $ is the machine precision. The optional integer value n specifies the number of successive iterations for which the criterion must be satisfied before the process terminates.

GCONV=r <n>
GTOL=r <n>

specifies a relative gradient convergence criterion. For all techniques except CONGRA and NMSIMP, termination requires that the normalized predicted function reduction be small,

\[ \frac{\mb{g}(\bpsi ^{(k)})^\prime [\bH ^{(k)}]^{-1} \mb{g}(\bpsi ^{(k)})}{|f(\bpsi ^{(k)})| } \leq r \]

where $\bpsi $ denotes the vector of parameters that participate in the optimization, $f(\cdot )$ is the objective function, and $\mb{g}(\cdot )$ is the gradient. For the CONGRA technique (where a reliable Hessian estimate, $\bH $, is not available), the following criterion is used:

\[ \frac{\parallel \mb{g}(\bpsi ^{(k)}) \parallel _2^2 \quad \parallel \mb{s}(\bpsi ^{(k)}) \parallel _2}{\parallel \mb{g}(\bpsi ^{(k)}) - \mb{g}(\bpsi ^{(k-1)}) \parallel _2 |f(\bpsi ^{(k)})| } \leq r \]

This criterion is not used by the NMSIMP technique. The default value is r = 1E–8. The optional integer value n specifies the number of successive iterations for which the criterion must be satisfied before the process terminates.

MAXFUNC=n
MAXFU=n

specifies the maximum number of function calls in the optimization process. The default values are as follows, depending on the optimization technique that you specify in the TECHNIQUE= option:

  • TRUREG, NRRIDG, NEWRAP: n = 125

  • QUANEW, DBLDOG: n = 500

  • CONGRA: n = 1,000

  • NMSIMP: n = 3,000

The optimization can terminate only after completing a full iteration. Therefore, the number of function calls that are actually performed can exceed n.

MAXITER=n
MAXIT=n

specifies the maximum number of iterations in the optimization process. The default values are as follows, depending on the optimization technique that you specify in the TECHNIQUE option:

  • TRUREG, NRRIDG, NEWRAP: n = 50

  • QUANEW, DBLDOG: n = 200

  • CONGRA: n = 400

  • NMSIMP: n = 1,000

These default values also apply when n is specified as a missing value.

MAXTIME=r

specifies an upper limit of r seconds of CPU time for the optimization process. The default value is the largest floating-point double representation of your computer. The time that you specify in this option is checked only once at the end of each iteration. Therefore, the actual running time can be longer than r.

MINITER=n
MINIT=n

specifies the minimum number of iterations. If you request more iterations than are actually needed for convergence to a stationary point, the optimization algorithms might behave strangely. For example, the effect of rounding errors can prevent the algorithm from continuing for the required number of iterations. By default, MINITER=0.

TECHNIQUE=keyword
TECH=keyword

specifies the optimization technique for obtaining smoothing parameter estimates and regression parameter estimates. You can choose from the following techniques:

CONGRA

performs a conjugate-gradient optimization.

DBLDOG

performs a version of double-dogleg optimization.

NEWRAP

performs a Newton-Raphson optimization with line search.

NMSIMP

performs a Nelder-Mead simplex optimization.

NONE

performs no optimization.

NRRIDG

performs a Newton-Raphson optimization with ridging.

QUANEW

performs a dual quasi-Newton optimization.

TRUREG

performs a trust-region optimization

By default, TECHNIQUE=NEWRAP for the performance iteration (METHOD= PERFORMANCE), and TECHNIQUE=QUANEW for the outer iteration (METHOD= OUTER).

For more information, see the section Choosing an Optimization Technique.