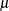The COUNTREG Procedure

MODEL Statement

Subsections:

Options for Variable Selection Based on an Information Criterion
Options for Penalized Variable Selection
Printing Options

MODEL dependent-variable = <regressors> </ options>;

The MODEL statement specifies the dependent-variable and independent covariates (regressors) for the regression model. If you specify no regressors, PROC COUNTREG fits a model that contains only an intercept. The dependent count variable should take on only nonnegative integer values in the input data set. PROC COUNTREG rounds any positive noninteger count values to the nearest integer and ignores any observations that have a negative count.

You can specify only one MODEL statement. You can specify the following options after a slash (/).

DIST=value

specifies the type of model to be analyzed. If you specify this option in both the MODEL statement and the PROC COUNTREG statement, then only the value in the MODEL statement is used. You can specify the following values:

CMPOISSON | C | CMP: specifies a Conway-Maxwell-Poisson regression model.
NEGBIN(P=1): specifies a negative binomial regression model that uses a linear variance function.
NEGBIN(P=2) | NEGBIN: specifies a negative binomial regression model that uses a quadratic variance function.
POISSON | P: specifies a Poisson regression model.
ZICMPOISSON | ZICMP: specifies a zero-inflated Conway-Maxwell-Poisson regression. You must also specify the ZEROMODEL statement when you specify this model type.
ZINEGBIN | ZINB: specifies a zero-inflated negative binomial regression. You must also specify the ZEROMODEL statement when you specify this model type.
ZIPOISSON | ZIP: specifies a zero-inflated Poisson regression. You must also specify the ZEROMODEL statement when you specify this model type.

ERRORCOMP=FIXED | RANDOM

specifies the type of conditional panel model to be analyzed. You can specify the following values:

FIXED: specifies a fixed-effect error component regression model.
RANDOM: specifies a random-effect error component regression model.

NOINT

suppresses the intercept parameter.

OFFSET=variable

specifies a variable in the input data set to be used as an offset variable. The offset variable appears as a covariate in the model with its parameter restricted to 1. The offset variable cannot be the response variable, the zero-inflation offset variable (if any), or one of the explanatory variables. The "Model Fit Summary" table gives the name of the data set variable used as the offset variable; it is labeled as "Offset."

PARAMETER=MU | LAMBDA

specifies the parameterization for the Conway-Maxwell-Poisson model. The following parameterizations are supported:

LAMBDA: estimates the original Conway-Maxwell-Poisson model (Shmueli et al. 2005).
MU: reparameterizes 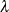$\lambda$ as documented by Guikema and Coffelt (2008), where 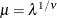$\mu =\lambda ^{1/{\nu }}$ and the integral part of $\mu$ represents the mode, which can be considered a measure of central tendency (mean).

By default, PARAMETER=MU.

Options for Variable Selection Based on an Information Criterion

For the MODEL, ZEROMODEL, DISPMODEL, SPATIALEFFECTS, SPATIALDISPEFFECTS, and SPATIALZEROEFFECTS statements, you can specify the following option after a slash (/) to control the variable selection process:

SELECT=INFO<(selection-options)> SELECTVAR=INFO<(selection-options)>

requests that the variable selection method be based on an information criterion. For more information, see the section Variable Selection Using an Information Criterion. You can specify one or more of the following selection-options:

DIRECTION=FORWARD | BACKWARD

specifies the search algorithm to use in the variable selection method. You can specify the following values:

FORWARD: specifies the search algorithm that starts with a base model and adds an additional variable at each step until either the model cannot be improved or one of the criteria for stopping has been met.
BACKWARD: specifies the search algorithm that starts with the original model and removes a variable at each step until either the model cannot be improved or one of the criteria for stopping has been met.

By default, DIRECTION=FORWARD.

CRITER=AIC | SBC

specifies the information criterion to use in the variable selection. You can specify the following values:

AIC: uses Akaike’s information criterion to determine whether the current model is better than the previous model.
SBC: uses the Schwarz-Bayesian information criterion to determine whether the current model is better than the previous model.

By default, CRITER=SBC.

LSTOP=percentage

specifies the percentage of decrease or increase in the AIC or SBC that is required for the algorithm to proceed; percentage must be a nonnegative number less than 1. By default, LSTOP=0.

MAXSTEPS=number

specifies the maximum number of steps to allow in the search algorithm. The default is infinite; that is, the algorithm does not stop until the stopping criterion is satisfied.

RETAIN(variable1 <variable2...>)

requests that the variables named within parentheses be retained during the variable selection process.

Options for Penalized Variable Selection

For the MODEL statement, you can specify the following option instead of the SELECT=INFO option:

SELECT=PEN<(selection-options)>

requests the penalized variable selection method. For more information, see the section Variable Selection Using an Information Criterion. You can specify one or more of the following selection-options:

GCV: specifies the generalized cross-validation (GCV) approach. For more information, see the section The GCV Approach.
GCV1: specifies the GCV1 approach. For more information, see the section The GCV1 Approach.
GCVLENGTH=value: specifies the number of different values to use for the generalized cross validation (GCV) tuning parameter. The value corresponds to $\lambda$
LAMBDA=value: specifies the value of lambda to use as the shrinkage parameter. When LAMBDA=0, no shrinkage is performed. As the value of LAMBDA increases, the coefficients are shrunk ever more strongly. By default, LAMBDA=0.
LLASTEPS=value: specifies the maximum number of iterations in the algorithm of local linear approximations. By default, LLASTEPS=5.

When SELECT=PEN, GCV1 is the default.

Printing Options

CORRB: prints the correlation matrix of the parameter estimates. The CORRB option can also be specified in the PROC COUNTREG statement.
COVB: prints the covariance matrix of the parameter estimates. The COVB can also be specified in the PROC COUNTREG statement.
ITPRINT: prints the objective function and parameter estimates at each iteration. The objective function is the negative log-likelihood function. The ITPRINT option can also be specified in the PROC COUNTREG statement.
PRINTALL: requests all printing options. The PRINTALL option can also be specified in the PROC COUNTREG statement.