The COUNTREG Procedure

Abramowitz, M., and Stegun, I. A., eds. (1970). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. 9th printing. New York: Dover.

Amemiya, T. (1985). Advanced Econometrics. Cambridge, MA: Harvard University Press.

Cameron, A. C., and Trivedi, P. K. (1986). “Econometric Models Based on Count Data: Comparisons and Applications of Some Estimators and Tests.” Journal of Applied Econometrics 1:29–53.

Cameron, A. C., and Trivedi, P. K. (1998). Regression Analysis of Count Data. Cambridge: Cambridge University Press.

Chan, J. C. C., and Eisenstat, E. (2015). “Marginal Likelihood Estimation with the Cross-Entropy Method.” Econometric Reviews 34:256–285.

Conway, R. W., and Maxwell, W. L. (1962). “A Queuing Model with State Dependent Service Rates.” Journal of Industrial Engineering 12:132–136.

Fan, J., and Li, R. (2001). “Variable Selection via Nonconcave Penalized Likelihood and Its Oracle Properties.” Journal of the American Statistical Association 96:1348–1360.

Gelman, A., Carlin, J. B., Stern, H. S., and Rubin, D. B. (2004). Bayesian Data Analysis. 2nd ed. London: Chapman & Hall.

Godfrey, L. G. (1988). Misspecification Tests in Econometrics. Cambridge: Cambridge University Press.

Greene, W. H. (1994). “Accounting for Excess Zeros and Sample Selection in Poisson and Negative Binomial Regression Models.” Working Paper 94-10, Department of Economics, Leonard N. Stern School of Business, New York University. http://ideas.repec.org/p/ste/nystbu/94-10.html.

Greene, W. H. (2000). Econometric Analysis. 4th ed. Upper Saddle River, NJ: Prentice-Hall.

Guikema, S. D., and Coffelt, J. P. (2008). “A Flexible Count Data Regression Model for Risk Analysis.” Risk Analysis 28:213–223.

Hausman, J. A., Hall, B. H., and Griliches, Z. (1984). “Econometric Models for Count Data with an Application to the Patents-R&D Relationship.” Econometrica 52:909–938.

King, G. (1989a). “A Seemingly Unrelated Poisson Regression Model.” Sociological Methods and Research 17:235–255.

King, G. (1989b). Unifying Political Methodology: The Likelihood Theory and Statistical Inference. Cambridge: Cambridge University Press.

Lambert, D. (1992). “Zero-Inflated Poisson Regression with an Application to Defects in Manufacturing.” Technometrics 34:1–14.

LaMotte, L. R. (1994). “A Note on the Role of Independence in t Statistics Constructed from Linear Statistics in Regression Models.” American Statistician 48:238–240.

Long, J. S. (1997). Regression Models for Categorical and Limited Dependent Variables. Thousand Oaks, CA: Sage Publications.

Lord, D., Guikema, S. D., and Geedipally, S. R. (2008). “Application of the Conway-Maxwell-Poisson Generalized Linear Model for Analyzing Motor Vehicle Crashes.” Accident Analysis and Prevention 40:1123–1134.

Park, M. Y., and Hastie, T. J. (2007). “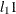-Regularization Path Algorithm for Generalized Linear Models.” Journal of the Royal Statistical Society, Series B 69:659–677.

Roberts, G. O., Gelman, A., and Gilks, W. R. (1997). “Weak Convergence and Optimal Scaling of Random Walk Metropolis Algorithms.” Annals of Applied Probability 7:110–120.

Roberts, G. O., and Rosenthal, J. S. (2001). “Optimal Scaling for Various Metropolis-Hastings Algorithms.” Statistical Science 16:351–367.

Schervish, M. J. (1995). Theory of Statistics. New York: Springer-Verlag.

Searle, S. R. (1971). Linear Models. New York: John Wiley & Sons.

Shmueli, G., Minka, T. P., Kadane, J. B., Borle, S., and Boatwright, P. (2005). “A Useful Distribution for Fitting Discrete Data: Revival of the Conway-Maxwell-Poisson Distribution.” Journal of the Royal Statistical Society, Series C 54:127–142.

Winkelmann, R. (2000). Econometric Analysis of Count Data. Berlin: Springer-Verlag.

Zou, H., and Li, R. (2008). “One-Step Sparse Estimates in Nonconcave Penalized Likelihood Models.” Annals of Statistics 36:1509–1533.