The COUNTREG Procedure

Spatial Lag of X Model

(Experimental)

The spatial lag of X (SLX) model is illustrated by using the general framework for a zero-inflated model. According to the section Zero-Inflated Count Regression Overview, the data model for 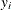$y_{i}$ can be formulated as

\[ y_ i \sim \left\{ \begin{array}{l@{\quad \mbox {with probability} \quad }l} 0 & \varphi _{i} \\ g(y_ i) & 1-\varphi _{i} \end{array} \right. \]

and the general model for parameters can be written in matrix form as

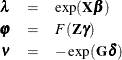
\begin{eqnarray*} \boldsymbol {\lambda }& =& \exp (\mathbf{X}\bbeta ) \\ \boldsymbol {\varphi }& =& F(\mathbf{Z}\bgamma ) \\ \boldsymbol {\nu }& =& -\exp (\mathbf{G}\boldsymbol {\delta }) \end{eqnarray*}

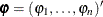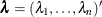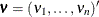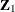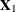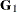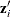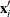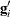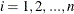where $\boldsymbol {\varphi }=(\varphi _{1},\ldots ,\varphi _{n})’$, $\boldsymbol {\lambda }=(\lambda _{1},\ldots ,\lambda _{n})’$, and $\boldsymbol {\nu }=(\nu _{1},\ldots ,\nu _{n})’$. In addition, $\mathbf{Z}_{1}$, $\mathbf{X}_{1}$, and $\mathbf{G}_{1}$ are design matrices, in which the ith row is $\mathbf{z}_{i}’$, $\mathbf{x}_{i}’$, and $\mathbf{g}_{i}’$ for $i=1,2,...,n$, respectively.

In the spatial context, data are often collected over a predetermined set of spatial units, 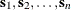$\mathbf{s}_{1},\mathbf{s}_{2},\ldots ,\mathbf{s}_{n}$. In this case, both the dependent variable and the explanatory variables are spatially referenced. For example, 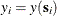$y_{i}=y(\mathbf{s}_{i})$ denotes the dependent variable that is observed at location $\mathbf{s}_{i}$. 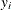For the SLX model, the data model for $y_{i}$ remains the same. However, the parameter model becomes

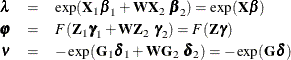
\begin{eqnarray*} \boldsymbol {\lambda }& =& \exp (\mathbf{X}_{1}\bbeta _{1} + \mathbf{W}\mathbf{X}_{2}\ \bbeta _{2})=\exp (\mathbf{X}\bbeta ) \\ \boldsymbol {\varphi }& =& F(\mathbf{Z}_{1}\bgamma _{1} + \mathbf{W}\mathbf{Z}_{2}\ \bgamma _{2})=F(\mathbf{Z}\bgamma ) \\ \boldsymbol {\nu }& =& -\exp (\mathbf{G}_{1}\boldsymbol {\delta }_{1} + \mathbf{W}\mathbf{G}_{2}\ \boldsymbol {\delta }_{2})=-\exp (\mathbf{G}\boldsymbol {\delta }) \end{eqnarray*}

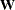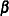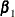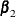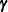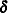where $\mathbf{W}$ is the spatial weights matrix, $\mathbf{X}=[\mathbf{X}_{1} \ \mathbf{W}\mathbf{X}_{2}]$, $\mathbf{Z}=[\mathbf{Z}_{1} \ \mathbf{W}\mathbf{Z}_{2}]$, and $\mathbf{G}=[\mathbf{G}_{1} \ \mathbf{W}\mathbf{G}_{2}]$. Moreover, $\bbeta $ becomes a column vector by stacking $\bbeta _{1}$ on top of $\bbeta _{2}$, and similarly for $\bgamma $ and $\boldsymbol {\delta }$. 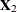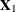For the sake of flexibility, $\mathbf{X}_{2}$ does not have to be the same as $\mathbf{X}_{1}$. Similar arguments apply to the DISPMODEL and ZEROMODEL statements. 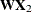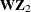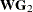From the modeling perspective, the SLX model can be useful when spatial effects (as represented by the $\mathbf{W}\mathbf{X}_{2}$, $\mathbf{W}\mathbf{Z}_{2}$, and $\mathbf{W}\mathbf{G}_{2}$ terms) are important. 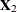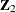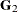The intercept term is always excluded from the design matrix $\mathbf{X}_{2}$, $\mathbf{Z}_{2}$, or $\mathbf{G}_{2}$.

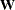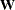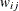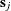A spatial weights matrix $\mathbf{W}$ is a square matrix, which often has nonnegative entries and its dimension is the total number of unique spatial units. Moreover, the diagonal elements of $\mathbf{W}$ are zeros because a spatial unit is not considered to be its own neighbor. Furthermore, the spatial weight $w_{ij}$ between locations $\mathbf{s}_{i}$ and $\mathbf{s}_{j}$ describes how much influence the spatial unit 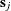$\mathbf{s}_{j}$ has on $\mathbf{s}_{i}$. 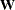In practice, $\mathbf{W}$ is often row-normalized; thus 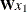$\mathbf{W}x_{1}$ can be interpreted as the spatially weighted average of $x_{1}$.

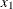In the SLX model, missing spatial weights are not allowed unless the NORMALIZE option is specified, in which case missing spatial weights are replaced by zeros. In addition, missing values are not allowed for the variables (including both dependent and explanatory variables) in the primary data set (which is specified in the DATA= option in the PROC COUNTREG statement).

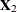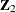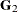The SPATIALEFFECTS , SPATIALZEROEFFECTS , and SPATIALDISPEFFECTS statements are used to include spatial effects in design matrices $\mathbf{X}_{2}$, $\mathbf{Z}_{2}$, and $\mathbf{G}_{2}$, respectively. Observations in the primary data set (specified in the DATA= option in the PROC COUNTREG statement) can be presented in different orders of spatial units than they are presented in the spatial weights data set (specified in the WMAT= option in the PROC COUNTREG statement). In this case, the SPATIALID statement enables you to use a spatial ID variable to associate the observations in the primary data set with those in the spatial weights data set. The SLX model is not supported for a panel data model.