The COUNTREG Procedure

Zero-Inflated Count Regression Overview

The main motivation for zero-inflated count models is that real-life data frequently display overdispersion and excess zeros. Zero-inflated count models provide a way of modeling the excess zeros in addition to allowing for overdispersion. In particular, for each observation, there are two possible data generation processes. The result of a Bernoulli trial is used to determine which of the two processes is used. For observation i, Process 1 is chosen with probability 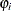$\varphi _{i}$ and Process 2 with probability 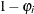$1-\varphi _{i}$. Process 1 generates only zero counts. Process 2 generates counts from either a Poisson or a negative binomial model. In general,

\[ y_ i \sim \left\{ \begin{array}{l@{\quad \mbox {with probability} \quad }l} 0 & \varphi _{i} \\ g(y_ i) & 1-\varphi _{i} \end{array} \right. \]

Therefore, the probability of 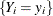$\{ Y_{i} = y_{i} \} $ can be described as

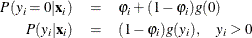
\begin{eqnarray*} P(y_{i}=0|\mathbf{x}_{i}) & = & \varphi _{i} + (1-\varphi _{i})g(0) \\ P(y_{i}|\mathbf{x}_{i}) & = & (1-\varphi _{i})g(y_{i}), \quad y_{i}>0 \end{eqnarray*}

where 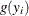$g(y_ i)$ follows either the Poisson or the negative binomial distribution. You can specify the probability 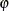$\varphi $ by using the PROBZERO= option in the OUTPUT statement.

When the probability 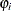$\varphi _{i}$ depends on the characteristics of observation i, 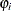$\varphi _{i}$ is written as a function of 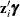$\mathbf{z}_{i}’\bgamma $, where 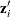$\mathbf{z}_ i’$ is the 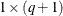$1 \times (q+1)$ vector of zero-inflation covariates and 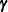$\bgamma $ is the 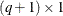$(q+1) \times 1$ vector of zero-inflation coefficients to be estimated. (The zero-inflation intercept is 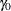$\gamma _0$; the coefficients for the q zero-inflation covariates are 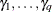$\gamma _1, \ldots , \gamma _ q$.) The function F that relates the product 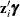$\mathbf{z}_{i}’\bgamma $ (which is a scalar) to the probability 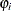$\varphi _{i}$ is called the zero-inflation link function,

\[ \varphi _{i} = F_{i} = F(\mathbf{z}_{i}’\bgamma ) \]

In the COUNTREG procedure, the zero-inflation covariates are indicated in the ZEROMODEL statement. Furthermore, the zero-inflation link function F can be specified as either the logistic function,

\[ F(\mathbf{z}_{i}’\bgamma ) = \Lambda (\mathbf{z}_{i}’\bgamma ) = \frac{\exp (\mathbf{z}_{i}'\bgamma )}{1+\exp (\mathbf{z}_{i}'\bgamma )} \]

or the standard normal cumulative distribution function (also called the probit function),

\[ F(\mathbf{z}_{i}’\bgamma ) = \Phi (\mathbf{z}_{i}’\bgamma ) = \int _{0}^{\mathbf{z}_{i}'\bgamma } \frac{1}{\sqrt {2 \pi }}\exp (-u^2 \slash 2) du \]

The zero-inflation link function is indicated in the LINK option in ZEROMODEL statement. The default ZI link function is the logistic function.