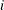Contents | SAS Program | PDF
The %MktBSize Macro
Introduction
The %MktBSize autocall macro suggests sizes for balanced incomplete block designs (BIBDs). The sizes that it reports meet necessary but not sufficient conditions for the existence of a BIBD, so a BIBD might not exist for every reported size.
Note: The version of the %MktBSize macro that is documented here requires SAS 940m1 or any subsequent release and the macro is included in the 940m3 release. An earlier version of the %MktBSize macro that is compatible with SAS 9.01 or any subsequent release is also available. The documentation for the earlier version of the macro is published at http://support.sas.com/rnd/app/macros/MktBSize_901/MktBSize_901.htm.
BIBD Parameters
The parameters of a BIBD are as follows:
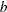 specifies the number of blocks. In a partial-profile design, this is the number of profiles. In a MaxDiff (best-worst) design, this is the number of sets.
specifies the number of blocks. In a partial-profile design, this is the number of profiles. In a MaxDiff (best-worst) design, this is the number of sets.  specifies the number of varieties or treatments. In a partial-profile or MaxDiff design, this is the total number of attributes or messages.
specifies the number of varieties or treatments. In a partial-profile or MaxDiff design, this is the total number of attributes or messages. 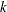 specifies the block size, which is the number of treatments in each block. In a partial-profile or MaxDiff design, this is the number of attributes or messages that are shown at one time.
specifies the block size, which is the number of treatments in each block. In a partial-profile or MaxDiff design, this is the number of attributes or messages that are shown at one time.
If 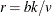 and
and 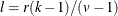 are integers, and
are integers, and 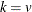 and
and 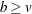 , then a complete block design might be possible. This is a necessary but not sufficient condition for the existence of a complete block design. If
, then a complete block design might be possible. This is a necessary but not sufficient condition for the existence of a complete block design. If 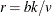 and
and 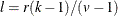 are integers, and
are integers, and 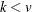 and
and 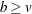 , then a balanced incomplete block design might be possible. This is a necessary but not sufficient condition for the existence of a BIBD.
, then a balanced incomplete block design might be possible. This is a necessary but not sufficient condition for the existence of a BIBD.
%MktBSize Macro Syntax
%MktBSize(K=do-list, V=do-list <, optional arguments>)
Required Arguments
Optional Arguments
Help Option
You can specify either of the following to display the option names and simple examples of the macro syntax:
%mktbsize(help) %mktbsize(?)
%MktBSize Macro Notes
This macro specifies options nonotes throughout most of its execution. If you want to see all the notes, submit the following statement before running the macro:
%let mktopts = notes;
To see the macro version, submit the following statement before running the macro:
%let mktopts = version;
Examples
The following invocation of the %MktBSize macro requests a list of designs that have 12 treatments, between 4 and 8 treatments per block, and between 12 and 30 blocks:
%mktbsize(v=12, k=4 to 8, b=12 to 30)
The results are shown in Figure 1.
Figure 1: %MktBSize Output
You can use this information to create a BIBD by using the %MktBIBD macro as follows:
%mktbibd(v=12, k=6, b=22, seed=104)
There is no guarantee that the %MktBIBD macro will find a BIBD for every specification, but in this case it does, and it finds the design shown in Figure 2.
Figure 2: BIBD with V=12, K=6, B=22
| Balanced Incomplete Block Design |
| x1 | x2 | x3 | x4 | x5 | x6 |
|---|---|---|---|---|---|
| 10 | 6 | 8 | 11 | 12 | 7 |
| 12 | 9 | 3 | 8 | 1 | 6 |
| 6 | 3 | 7 | 1 | 5 | 12 |
| 1 | 3 | 2 | 4 | 8 | 9 |
| 3 | 10 | 12 | 5 | 2 | 4 |
| 8 | 10 | 2 | 7 | 9 | 5 |
| 6 | 8 | 5 | 10 | 9 | 3 |
| 11 | 7 | 6 | 2 | 3 | 9 |
| 7 | 8 | 1 | 12 | 4 | 10 |
| 9 | 4 | 12 | 6 | 5 | 11 |
| 8 | 5 | 11 | 10 | 3 | 1 |
| 3 | 4 | 7 | 9 | 11 | 10 |
| 2 | 9 | 11 | 1 | 10 | 12 |
| 12 | 7 | 8 | 3 | 2 | 11 |
| 7 | 11 | 4 | 5 | 1 | 3 |
| 10 | 6 | 4 | 3 | 12 | 2 |
| 5 | 12 | 9 | 8 | 11 | 4 |
| 5 | 2 | 6 | 7 | 4 | 8 |
| 4 | 1 | 10 | 9 | 6 | 7 |
| 2 | 11 | 1 | 4 | 8 | 6 |
| 1 | 5 | 10 | 11 | 6 | 2 |
| 9 | 2 | 5 | 12 | 7 | 1 |
The design has 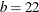 blocks (rows),
blocks (rows), 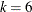 treatments per block (columns), and
treatments per block (columns), and 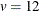 treatments (the entries are the integers 1 to 12). Each of the
treatments (the entries are the integers 1 to 12). Each of the 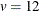 treatments occurs
treatments occurs 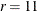 times, and each treatment occurs in a block with every other treatment
times, and each treatment occurs in a block with every other treatment 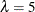 times.
times.
The following invocation of the %MktBSize macro creates a list of more than 50 designs:
%mktbsize(v=5 to 20, k=3 to v - 1, b=v to 30)
Figure 3 shows a partial listing of the results.
Figure 3: %MktBSize Output
By default, the maximum number of replications is 1 (MAXREPS=1). Therefore, the design in which 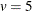 ,
, 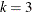 , and
, and 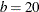 is not listed because it consists of two replications of the design in which
is not listed because it consists of two replications of the design in which 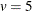 ,
, 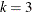 , and
, and 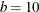 , which is listed. Also, the number of blocks (
, which is listed. Also, the number of blocks (b=v to 30) is specified so that it is never less than the number of treatments. Furthermore, the number of treatments per block (k=3 to v-1) is specified to always be less than the number of treatments. Even more complicated expressions are permitted. For example, to limit the number of treatments per block to no more than half the number of treatments, you could specify
%mktbsize(v=2 to 10, k=2 to 0.5 * v, b=v to 10)
To limit the number of blocks as a function of the number of treatments, you could specify
%mktbsize(v=2 to 10, k=2 to v - 1, b=v to 2 * v)
However, if you want to limit the number of treatments as a function of the number of blocks, you need to use the ORDER= argument to ensure that the number-of-blocks loop comes first, as in the following specification:
%mktbsize(b=2 to 10, v=2 to 0.5 * b, k=2 to v - 1, order=bvk)
The macro reports sizes in which 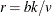 and
and 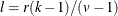 are integers,
are integers, 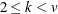 , and
, and 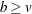 . If
. If 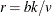 and
and 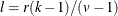 are integers, and
are integers, and 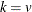 and
and 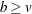 , then a complete block design might be possible. This is a necessary but not sufficient condition for the existence of a complete block design. If
, then a complete block design might be possible. This is a necessary but not sufficient condition for the existence of a complete block design. If 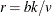 and
and 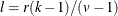 are integers, and
are integers, and 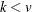 and
and 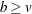 , then a balanced incomplete block design might be possible. This is a necessary but not sufficient condition for the existence of a BIBD. If you specify OPTIONS=UBD and
, then a balanced incomplete block design might be possible. This is a necessary but not sufficient condition for the existence of a BIBD. If you specify OPTIONS=UBD and 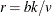 is an integer, then the %MktBSize macro reports unbalanced block design sizes along with BIBD sizes. For example, if you want a design that has 20 treatments and a block size of 6, you can use the following invocation of the %MktBSize macro to find out how many blocks you need:
is an integer, then the %MktBSize macro reports unbalanced block design sizes along with BIBD sizes. For example, if you want a design that has 20 treatments and a block size of 6, you can use the following invocation of the %MktBSize macro to find out how many blocks you need:
%mktbsize(v=20, k=6, options=ubd)
Figure 4 displays the results.
Figure 4: %MktBSize Output
You can then use the %MktBIBD macro to find a design in which each treatment occurs three times but the treatments do not appear together an equal number of times, as in the following example:
%mktbibd(v=20, k=6, b=10, seed=104)
Figure 5 shows the treatment-by-treatment frequencies and the design.
Figure 5: %MktBIBD Output
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 1 | 0 | 0 | 2 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 2 | 0 | 1 | 0 | 1 | 1 | 1 |
| 2 | . | 3 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 2 | 1 |
| 3 | . | . | 3 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 2 | 2 | 1 | 1 | 0 |
| 4 | . | . | . | 3 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 2 | 0 |
| 5 | . | . | . | . | 3 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 2 | 0 | 0 | 1 | 0 |
| 6 | . | . | . | . | . | 3 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 7 | . | . | . | . | . | . | 3 | 1 | 0 | 0 | 2 | 2 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| 8 | . | . | . | . | . | . | . | 3 | 1 | 1 | 1 | 1 | 2 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 9 | . | . | . | . | . | . | . | . | 3 | 1 | 0 | 1 | 2 | 0 | 1 | 1 | 1 | 1 | 0 | 2 |
| 10 | . | . | . | . | . | . | . | . | . | 3 | 0 | 1 | 0 | 1 | 2 | 1 | 0 | 1 | 1 | 1 |
| 11 | . | . | . | . | . | . | . | . | . | . | 3 | 1 | 1 | 2 | 1 | 0 | 1 | 1 | 0 | 1 |
| 12 | . | . | . | . | . | . | . | . | . | . | . | 3 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 13 | . | . | . | . | . | . | . | . | . | . | . | . | 3 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 14 | . | . | . | . | . | . | . | . | . | . | . | . | . | 3 | 1 | 1 | 1 | 1 | 0 | 1 |
| 15 | . | . | . | . | . | . | . | . | . | . | . | . | . | . | 3 | 0 | 1 | 1 | 1 | 1 |
| 16 | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | 3 | 1 | 1 | 1 | 0 |
| 17 | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | 3 | 1 | 1 | 1 |
| 18 | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | 3 | 1 | 2 |
| 19 | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | 3 | 0 |
| 20 | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | . | 3 |