The TPSPLINE Procedure
MODEL Statement
-
MODEL dependent-variables = <regression-variables> (smoothing-variables)</ options>;
The MODEL statement specifies the dependent variables, the independent regression variables, which are listed with no parentheses, and the independent smoothing variables, which are listed inside parentheses.
The regression variables are optional. At least one smoothing variable is required, and it must be listed after the regression variables. No variables can be listed in both the regression variable list and the smoothing variable list.
If you specify more than one dependent variable, PROC TPSPLINE calculates a thin-plate smoothing spline estimate for each dependent variable by using the regression variables and smoothing variables specified on the right side.
If you specify regression variables, PROC TPSPLINE fits a semiparametric model by using the regression variables as the linear part of the model.
Table 116.3 summarizes the options available in the MODEL statement.
Table 116.3: MODEL Statement Options
|
Option |
Description |
|---|---|
|
Specifies the significance level |
|
|
Specifies the degrees of freedom |
|
|
Defines a range in which points are treated as replicates |
|
|
Specifies the smoothing parameter |
|
|
Specifies a set of values for the |
|
|
Specifies the smoothing parameter on the |
|
|
Specifies a set of values for the |
|
|
Specifies the order of the derivative |
|
|
Specifies the range for smoothing values to be evaluated |
You can specify the following options in the MODEL statement:

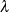
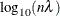

![\[ \Argument{df}=\mr{tr}(\mb{A}(\lambda )) \]](images/statug_tpspline0036.png)
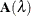
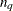




![\[ \| \mb{x}_{i}-\mb{x}_{j}\| _{\infty } \leq D/2 \]](images/statug_tpspline0042.png)















