The TPSPLINE Procedure

Andrews, D. W. K. (1988). Asymptotic Optimality of Generalized 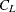, Cross-validation, and Generalized Cross-validation in Regression with Heteroskedastic Errors. Cowles Foundation Discussion Paper 906, Cowles Foundation for Research in Economics at Yale University. Revised May 1989.

Bates, D. M., Lindstrom, M. J., Wahba, G., and Yandell, B. S. (1987). “GCVPACK-Routines for Generalized Cross Validation.” Communications in Statistics—Simulation and Computation 16:263–297.

Cleveland, W. S. (1993). Visualizing Data. Summit, NJ: Hobart Press.

Dongarra, J. J., Bunch, J. R., Moler, C. B., and Steward, G. W. (1979). Linpack Users’ Guide. Philadelphia: Society for Industrial and Applied Mathematics.

Duchon, J. (1976). “Fonctions-spline et espérances conditionnelles de champs gaussiens.” Annales scientifiques de l’Université de Clermont-Ferrand 2, Série Mathématique 14:19–27.

Duchon, J. (1977). “Splines Minimizing Rotation-Invariant Semi-norms in Sobolev Spaces.” In Constructive Theory of Functions of Several Variables, edited by W. Schempp, and K. Zeller, 85–100. New York: Springer-Verlag.

Hall, P., and Titterington, D. M. (1987). “Common Structure of Techniques for Choosing Smoothing Parameters in Regression Problems.” Journal of the Royal Statistical Society, Series B 49:184–198.

Houghton, A. N., Flannery, J., and Viola, M. V. (1980). “Malignant Melanoma in Connecticut and Denmark.” International Journal of Cancer 25:95–104.

Hutchinson, M., and Bischof, R. (1983). “A New Method for Estimating the Spatial Distribution of Mean Seasonal and Annual Rainfall Applied to the Hunter Valley.” Australian Meteorological Magazine 31:179–184.

Meinguet, J. (1979). “Multivariate Interpolation at Arbitrary Points Made Simple.” Journal of Applied Mathematics and Physics 30:292–304.

Nychka, D. (1986a). The Average Posterior Variance of a Smoothing Spline and a Consistent Estimate of the Mean Square Error. Technical Report 168, North Carolina State University.

Nychka, D. (1986b). A Frequency Interpretation of Bayesian "Confidence" Interval for Smoothing Splines. Technical Report 169, North Carolina State University.

Nychka, D. (1988). “Bayesian Confidence Intervals for Smoothing Splines.” Journal of the American Statistical Association 83:1134–1143.

O’Sullivan, F., and Wong, T. (1987). Determining a Function Diffusion Coefficient in the Heat Equation. Technical report, Department of Statistics, University of California, Berkeley.

Ramsay, J. O., and Silverman, B. W. (1997). Functional Data Analysis. New York: Springer-Verlag.

Seaman, R., and Hutchinson, M. (1985). “Comparative Real Data Tests of Some Objective Analysis Methods by Withholding.” Australian Meteorological Magazine 33:37–46.

Villalobos, M., and Wahba, G. (1987). “Inequality Constrained Multivariate Smoothing Splines with Application to the Estimation of Posterior Probabilities.” Journal of the American Statistical Association 82:239–248.

Wahba, G. (1983). “Bayesian 'Confidence Intervals' for the Cross Validated Smoothing Spline.” Journal of the Royal Statistical Society, Series B 45:133–150.

Wahba, G. (1990). Spline Models for Observational Data. Philadelphia: Society for Industrial and Applied Mathematics.

Wahba, G., and Wendelberger, J. (1980). “Some New Mathematical Methods for Variational Objective Analysis Using Splines and Cross Validation.” Monthly Weather Review 108:1122–1145.

Wang, Y., and Wahba, G. (1995). “Bootstrap Confidence Intervals for Smoothing Splines and Their Comparison to Bayesian Confidence Intervals.” Journal of Statistical Computation and Simulation 51:263–279.