The QUANTLIFE Procedure

Confidence Interval

Subsections:

Direct computation of the covariance of the parameter estimators involves a complicated density estimation. Instead, the QUANTLIFE procedure computes confidence intervals for the quantile regression parameters 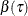${\beta }(\tau )$ by using resampling methods. The QUANTLIFE procedure implements two different methods, the exponentially weighted method and the pairwise resampling method.

Exponentially Weighted Method

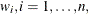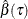This method samples weights $w_ i, i=1, \ldots , n,$ from a standard exponential distribution that has mean 1 and variance 1. Then it computes the censored quantile regression estimators $\hat\beta (\tau )$ based on the observed data 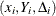$(x_ i,Y_ i, \Delta _ i)$ with the weights 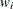$w_ i$. These steps are repeated B times (where B is the value of the NREP= option in the PROC QUANTLIFE statement). The confidence intervals can be obtained from these B estimates. You can specify this method by using the CI=EW option in the PROC QUANTLIFE statement.

Pairwise Method

This method samples 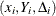$(x_ i,Y_ i, \Delta _ i)$ with replacement and computes the quantile regression estimators 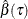$\hat\beta (\tau )$ based on the resampled data. These steps are repeated B times (where B is the value of the NREP= option in the PROC QUANTLIFE statement). The confidence intervals can be obtained from these B estimates. You can specify this method by using the CI=PW option in the PROC QUANTLIFE statement.

Testing Effects of Covariates

Consider the linear model

\[ y_ i =\mb{x}_{1i}^{\prime }\bbeta _1 + \mb{x}_{2i}^{\prime }\bbeta _2 + \epsilon _ i \]

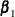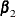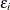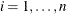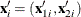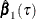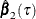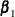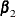where $\bbeta _1$ and $\bbeta _2$ are p-dimensional and q-dimensional parameters, respectively, and $\epsilon _ i$, $i=1,\ldots ,n$, are errors. Denote $\mb{x}_ i^{\prime }=(\mb{x}_{1i}^{\prime }, \mb{x}_{2i}^{\prime })$, and let $\hat\bbeta _1(\tau )$ and $\hat\bbeta _2(\tau )$ be the parameter estimates for $\bbeta _1$ and $\bbeta _2$, respectively, at the $\tau $th quantile.

The QUANTLIFE procedure implements the Wald test for the null hypothesis:

\[ H_{0}: \beta _2(\tau ) = 0 \]

The Wald test statistic, which is based on the estimated coefficients 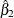$\hat\beta _2$ from the unrestricted fitted model, is given by

\[ T_ W(\tau ) = {\hat\beta _2^{\prime }(\tau )} {\hat\Sigma (\tau )}^{-1} {\hat\beta _2(\tau )} \]

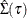where ${\hat\Sigma (\tau )}$ is an estimator of the covariance of 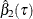${\hat\beta _2(\tau )}$, which is obtained by using resampling methods.