The QUANTLIFE Procedure

Nelson-Aalen-Type Estimator for Censored Quantile Regression

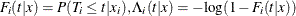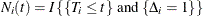Peng and Huang (2008) propose a method of censored quantile regression that is based on the Nelson-Aalen estimator of the cumulative hazard function. Let $F_ i(t |x) = P(T_ i\le t | x_ i), \Lambda _ i(t|x) = -\mr{log}(1 - F_ i(t|x))$, and $N_ i(t) = I\left\{ \left\{ T_ i \le t\} \mbox{ and } \{ \Delta _ i=1\right\} \right\} $. Then the following equation is a martingale process that is associated with the counting process 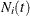$N_ i(t)$ (Fleming and Harrington 1991):

\[ M_ i(t) = N_ i(t) - \Lambda _ i(t \wedge Y_ i |x) \]

Based on the martingale process, Peng and Huang (2008) derive the following estimating equation:

\[ n^{-1/2} \sum _{i=1}^ n x_ i[N_ i(\mr{exp}(x_ i’\beta (\tau )))- \int _{0}^{\tau }I(Y_ i \ge \mr{exp}(x_ i’\beta (\tau )))d H(u)]=0 \]

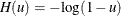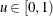where $H(u)=-\mr{log}(1-u)$ and $u \in [0,1)$. By approximating the integral in the estimating equation on a grid 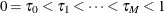$0=\tau _0 < \tau _1 < \cdots < \tau _ M < 1$, the regression quantiles 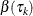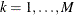$\beta (\tau _ k)$, $k=1, \ldots , M$, can be estimated sequentially by solving the following linear programming problem:

\[ \min _{b} \{ \alpha (\tau _ k) ’ u +(\Delta - \alpha (\tau _ k)) ’ v \mbox{ } |\mbox{ }z= Xb + u- v, u \ge 0, v \ge 0\} \]

where

\[ \alpha (\tau _ k)= \sum _{j=1}^{k-1} I(Y_ i \ge \mr{exp}(x_ i’\hat\beta (\tau _ j)))H((u_{j+1})-H(u_ j)) \]

and X is the known matrix of 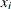$x_ i$’s. For more information, see Koenker (2008).

You can request this method by specifying the METHOD=NA option. The grid points 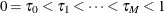$0=\tau _0 < \tau _1 < \cdots < \tau _ M < 1$ are equally spaced, with 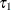$\tau _1$ specified by the INITTAU=option and the grid step between two adjacent grid points specified by the GRIDSIZE=option.