The QUANTLIFE Procedure

Notation for Censored Quantile Regression

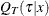Let T be a dependent variable, such as a survival time, and let x be a p $\times $ 1 covariate vector. Quantile regression methods focus on modeling the conditional quantile function, $Q_ T(\tau |x)$, which is defined as

\[ Q_ T(\tau |x)=\mbox{inf} \{ t: P(T\le t|x)=\tau \} ,\, 0<\tau <1 \]

For example, 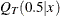$Q_ T(0.5|x)$ is the conditional median quantile, and 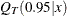$Q_ T(0.95|x)$ is the conditional quantile function that corresponds to the 95th percentile.

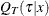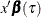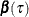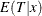A linear quantile regression model for $Q_ T(\tau |x)$ has the form $x ^{\prime } \bbeta (\tau )$. One of the advantages of quantile regression analysis is that the covariate effect $\bbeta (\tau )$ can change with $\tau $. Unlike ordinary least squares regression, which estimates the conditional expectation function $E(T|x)$, quantile regression offers the flexibility to model the entire conditional distribution.

Given observations 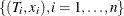$\{ (T_ i,x_ i), i=1, \ldots , n\} $, standard quantile regression estimates the regression coefficients 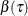$\beta (\tau )$ by minimizing the following objective function over b:

\[ r(b) = \sum _{i=1}^ n \rho _\tau ( T_ i - x_ i^{\prime } \, b ) \]

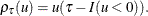
where $\rho _\tau ( u ) = u ( \tau - I(u<0)).$

However, in many applications, the responses 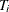$T_ i$ are subject to censoring. For example, in a biomedical study, censoring occurs when patients withdraw from the study or die from a cause that is unrelated to the disease being studied.

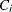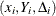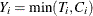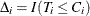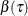Let $C_ i$ denote the censoring variable. In the case of right-censoring, the triples $(x_ i,Y_ i, \Delta _ i)$ are observed, where $Y_ i = \mbox{min}(T_ i,C_ i)$ and $\Delta _ i = I(T_ i \le C_ i)$ are the observed response variable and the censoring indicator, respectively. Standard quantile regression can lead to a biased estimator of the regression parameters $\beta (\tau )$ when censoring occurs.

The following sections describe two methods for estimating the quantile coefficient 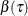$\beta (\tau )$ in the presence of right-censoring.