The QUANTLIFE Procedure

Kaplan-Meier-Type Estimator for Censored Quantile Regression

Portnoy (2003) proposes the use of weighted quantile regression to sequentially estimate 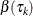$\beta (\tau _ k)$ along the equally spaced grid 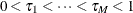$0 < \tau _1 < \cdots < \tau _ M < 1$. You can request this method by specifying the METHOD=KM option in the PROC QUANTLIFE statement. The grid points 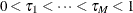$0< \tau _1 < \cdots < \tau _ M < 1$ are equally spaced, with 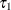$\tau _1$ specified by the INITTAU= option and the step between adjacent grid points specified by the GRIDSIZE=option.

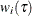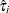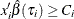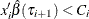This method uses a weight function $w_{i}(\tau )$ for each censored observation. The weight function is constructed as follows: Let $\hat\tau _{i}$ be the first grid point at which $x_ i^{\prime }\hat\beta (\tau _{i}) \ge C_ i$ and $x_ i^{\prime } \hat\beta (\tau _{i+1}) < C_ i$; otherwise let 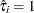$\hat\tau _{i} = 1$. 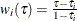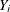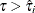When computing the $\tau $th quantile, assign weight $w_{i}(\tau ) = \frac{\tau -\hat\tau _ i}{1-\hat\tau _ i}$ to the censored observation $Y_ i$ if $\tau >\hat\tau _{i}$; otherwise assign 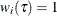$w_{i}(\tau ) =1$. The algorithm for computing 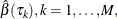$\hat\beta (\tau _ k), k=1, \ldots ,M,$ is as follows:

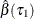  1. Compute $\hat\beta (\tau _1)$ by using the standard quantile regression method.

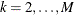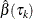  2. For $k=2, \ldots , M$, obtain $\hat\beta (\tau _{k})$ sequentially by minimizing the following weighted quantile regression objective function:

    \[ \begin{array}{lll} r_ w(b) & =\sum _{\Delta _ i=1} \rho _{\tau _ k}(Y_ i - {x}_ i’ { b})\\ & +\sum _{\Delta _ i=0} \left\{ w_{i}(\tau _ k) \, \rho _{\tau _ k}(Y_ i - {x}_ i’ b) + (1 - w_{i}(\tau _ k)) \rho _{\tau _ k}(Y^* - { x}_ i’ b) \right\} \end{array} \]

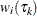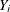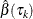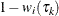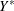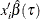    where $w_{i}(\tau _ k)$ is the weight for the right-censored observation $Y_ i$ at computing $\hat\beta (\tau _ k)$, and the complementary weight $1-w_{i}(\tau _ k)$ is for $Y^*$, a large constant that is greater than all $x_ i’\hat\beta (\tau )$.

The weighted quantile regression method is similar to Efron’s redistribution-of-mass idea (Efron 1967) for the Kaplan-Meier estimator.

Note that if all observations are uncensored, 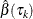$\hat\beta (\tau _ k)$ is the same as the standard quantile regression estimator.