The QUANTLIFE Procedure
Relationship of Quantile Function and Survival Function
Both quantile function and survival function are useful in characterizing a lifetime distribution.
By the definition of the quantile function 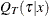 ,
,
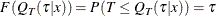
In other words, the cumulative distribution function 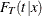 maps
maps 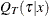 to
to  , and thus the corresponding survival function
, and thus the corresponding survival function 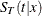 maps
maps 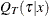 to
to 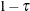 .
.
When you specify the LOG option, the QUANTLIFE procedure fits a linear quantile regression model for a log transformation of the lifetime as
![\[ Q_{\mr{log}(T)} (\tau |x)=x’\bbeta (\tau ) \]](images/statug_quantlife0084.png)
where 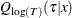 is the
is the  th quantile of
th quantile of 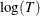 at x. The estimated quantile function for T given x is
at x. The estimated quantile function for T given x is 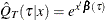 , because the quantile function is invariant under a monotone transformation.
, because the quantile function is invariant under a monotone transformation.
You can specify the covariates x in the COVARIATES= data set of the BASELINE statement and the PLOTS=(QUANTILE SURVIVAL) option in the PROC statement. Then
the conditional quantile function at x is plotted as 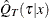 against
against  , and the conditional survival function at x is plotted as
, and the conditional survival function at x is plotted as 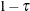 against
against 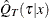 .
.
