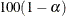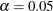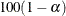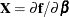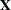The NLIN Procedure

OUTPUT Statement

OUTPUT OUT=SAS-data-set keyword=names <…keyword=names> </ options>;

The OUTPUT statement specifies an output data set to contain statistics calculated for each observation. For each statistic, specify the keyword, an equal sign, and a variable name for the statistic in the output data set. All of the names appearing in the OUTPUT statement must be valid SAS names, and none of the new variable names can match a variable already existing in the data set to which PROC NLIN is applied.

If an observation includes a missing value for one of the independent variables, both the predicted value and the residual value are missing for that observation. If the iterations fail to converge, all the values of all the variables named in the OUTPUT statement are missing values.

Table 81.6 summarizes the options available in the OUTPUT statement.

Table 81.6: OUTPUT Statement Options

Option	Description
Output data set and OUTPUT statement options
ALPHA=	Specifies the level of significance $\alpha$
DER	Saves the first derivatives of the model
OUT=	Specifies the output data set
Keyword options
H=	Specifies the tangential leverage
J=	Specifies the Jacobian leverage
L95=	Specifies the lower bound of an approximate 95% prediction interval
L95M=	Specifies the lower bound of an approximate 95% confidence interval for the mean
LCL=	Specifies the lower bound of an approximate $100(1 - \alpha )$ % prediction interval
LCLM=	Specifies the lower bound of an approximate $100(1 - \alpha )$ % confidence interval for the mean
LMAX=	Specifies the direction of maximum local influence
PARMS=	Specifies the parameter estimates
PREDICTED=	Specifies the predicted values
PROJRES=	Specifies the projected residuals
PROJSTUDENT=	Specifies the standardized projected residuals
RESEXPEC=	Specifies the mean of the residuals
RESIDUAL=	Specifies the residuals
SSE=	Specifies the residual sum of squares
STDI=	Specifies the standard error of the individual predicted value
STDP=	Specifies the standard error of the mean predicted value
STDR=	Specifies the standard error of the residual
STUDENT=	Specifies the standardized residuals
U95=	Specifies the upper bound of an approximate 95% prediction interval
U95M=	Specifies the upper bound of an approximate 95% confidence interval for the mean
UCL=	Specifies the upper bound of an approximate $100(1 - \alpha )$ % prediction interval
UCLM=	Specifies the upper bound of an approximate $100(1 - \alpha )$ % confidence interval for the mean
WEIGHT=	Specifies the special variable `_WEIGHT_`

You can specify the following options in the OUTPUT statement. For a description of computational formulas, see Chapter 4: Introduction to Regression Procedures.

OUT=SAS-data-set: specifies the SAS data set to be created by PROC NLIN when an OUTPUT statement is included. The new data set includes the variables in the input data set. Also included are any ID variables specified in the ID statement, plus new variables with names that are specified in the OUTPUT statement.

The following values can be calculated and output to the new data set.

H=name: specifies a variable that contains the tangential leverage. See the section Leverage in Nonlinear Regression for details.
J=name: specifies a variable that contains the Jacobian leverage. See the section Leverage in Nonlinear Regression for details.
L95=name: specifies a variable that contains the lower bound of an approximate 95% confidence interval for an individual prediction. This includes the variance of the error as well as the variance of the parameter estimates. See also the description for the U95= option later in this section.
L95M=name: specifies a variable that contains the lower bound of an approximate 95% confidence interval for the expected value (mean). See also the description for the U95M= option later in this section.
LCL=name: specifies a variable that contains the lower bound of an approximate $100(1 - \alpha )$ % confidence interval for an individual prediction. The $\alpha$ level is equal to the value of the ALPHA= option in the OUTPUT statement or, if this option is not specified, to the value of the ALPHA= option in the PROC NLIN statement. If neither of these options is specified, then $\alpha =0.05$ by default, resulting in a lower bound for an approximate 95% confidence interval. For the corresponding upper bound, see the UCL keyword.
LCLM=name: specifies a variable that contains the lower bound of an approximate $100(1 - \alpha )$ % confidence interval for the expected value (mean). The $\alpha$ level is equal to the value of the ALPHA= option in the OUTPUT statement or, if this option is not specified, to the value of the ALPHA= option in the PROC NLIN statement. If neither of these options is specified, then $\alpha =0.05$ by default, resulting in a lower bound for an approximate 95% confidence interval. For the corresponding lower bound, see the UCLM keyword.
LMAX=name: specifies a variable that contains the direction of maximum local influence of an additive perturbation of the response variable. See the section Local Influence in Nonlinear Regression for details.
PARMS=names: specifies variables in the output data set that contains parameter estimates. These can be the same variable names that are listed in the PARAMETERS statement; however, you can choose new names for the parameters identified in the sequence from the parameter estimates table. A note in the log indicates which variable in the output data set is associated with which parameter name. Note that, for each of these new variables, the values are the same for every observation in the new data set.
PREDICTED=name P=name: specifies a variable in the output data set that contains the predicted values of the dependent variable.
PROJRES=name: specifies a variable that contains the projected residuals obtained by projecting the residuals (ordinary residuals) into the null space of $(X|H)$ . For the ordinary residuals, see the RESIDUAL= option later in this section. The section Residuals in Nonlinear Regression describes the statistical properties of projected residuals in nonlinear regression.
PROJSTUDENT=name: specifies a variable that contains the standardized projected residuals. See the section Residuals in Nonlinear Regression for details and the STUDENT= option later in this section.
RESEXPEC=name: specifies a variable that contains the mean of the residuals. In contrast to linear regressions where the mean of the residuals is zero, in nonlinear regression the residuals have a nonzero mean value and show a negative covariance with the mean response. See the section Residuals in Nonlinear Regression for details.
RESIDUAL=name R=name: specifies a variable in the output data set that contains the residuals. See also the description of PROJRES= option stated previously in this section and the section Residuals in Nonlinear Regression for the statistical properties of residuals and projected residuals.
SSE=name ESS=name: specifies a variable in the output data set that contains the residual sum of squares finally determined by the procedure. The value of the variable is the same for every observation in the new data set.
STDI=name: specifies a variable that contains the standard error of the individual predicted value.
STDP=name: specifies a variable that contains the standard error of the mean predicted value.
STDR=name: specifies a variable that contains the standard error of the residual.
STUDENT=name: specifies a variable that contains the standardized residuals. These are residuals divided by their estimated standard deviation. See the PROJSTUDENT= option defined previously in this section and the section Residuals in Nonlinear Regression for the statistical properties of residuals and projected residuals.
U95=name: specifies a variable that contains the upper bound of an approximate 95% confidence interval for an individual prediction. See also the description for the L95= option.
U95M=name: specifies a variable that contains the upper bound of an approximate 95% confidence interval for the expected value (mean). See also the description for the L95M= option.
UCL=name: specifies a variable that contains the upper bound of an approximate $100(1 - \alpha )$ % confidence interval an individual prediction. The $\alpha$ level is equal to the value of the ALPHA= option in the OUTPUT statement or, if this option is not specified, to the value of the ALPHA= option in the PROC NLIN statement. If neither of these options is specified, then $\alpha =0.05$ by default, resulting in an upper bound for an approximate 95% confidence interval. For the corresponding lower bound, see the LCL keyword.
UCLM=name: specifies a variable that contains the upper bound of an approximate $100(1 - \alpha )$ % confidence interval for the expected value (mean). The $\alpha$ level is equal to the value of the ALPHA= option in the OUTPUT statement or, if this option is not specified, to the value of the ALPHA= option in the PROC NLIN statement. If neither of these options is specified, then $\alpha =0.05$ by default, resulting in an upper bound for an approximate 95% confidence interval. For the corresponding lower bound, see the LCLM keyword.
WEIGHT=name: specifies a variable in the output data set that contains values of the special variable _WEIGHT_.

You can specify the following options in the OUTPUT statement after a slash (/) :

ALPHA= $\alpha$

specifies the level of significance $\alpha$ for $100(1-\alpha )$ % confidence intervals. By default, $\alpha$ is equal to the value of the ALPHA= option in the PROC NLIN statement or 0.05 if that option is not specified. You can supply values that are strictly between 0 and 1.

DER

saves the first derivatives of the model with respect to the parameters to the OUTPUT data set. The derivatives are named DER_parmname, where "parmname" is the name of the model parameter in your NLIN statements. You can use the DER option to extract the $\mb{X} = \partial \mb{f}/\partial \bbeta$ matrix into a SAS data set. For example, the following statements create the data set nlinX, which contains the $\mb{X}$ matrix:

proc nlin;
   parms theta1=155 theta3=0.04;
   model V = theta1*c / (theta3 + c);
   output out=nlinout / der;
run;

data nlinX;
   set nlinout(keep=DER_:);
run;

The derivatives are evaluated at the final parameter estimates.