The NLIN Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Automatic DerivativesMeasures of Nonlinearity, Diagnostics and InferenceMissing ValuesSpecial VariablesTroubleshootingComputational MethodsOutput Data SetsConfidence IntervalsCovariance Matrix of Parameter EstimatesConvergence MeasuresDisplayed OutputIncompatibilities with SAS 6.11 and Earlier Versions of PROC NLINODS Table NamesODS Graphics
Automatic DerivativesMeasures of Nonlinearity, Diagnostics and InferenceMissing ValuesSpecial VariablesTroubleshootingComputational MethodsOutput Data SetsConfidence IntervalsCovariance Matrix of Parameter EstimatesConvergence MeasuresDisplayed OutputIncompatibilities with SAS 6.11 and Earlier Versions of PROC NLINODS Table NamesODS Graphics -
Examples

- References
Example 81.2 Iteratively Reweighted Least Squares
With the NLIN procedure you can perform weighted nonlinear least squares regression in situations where the weights are functions
of the parameters. To minimize a weighted sum of squares, you assign an expression to the _WEIGHT_ variable in your PROC NLIN statements. When the _WEIGHT_ variable depends on the model parameters, the estimation technique is known as iteratively reweighted least squares (IRLS).
In this situation you should employ the NOHALVE
option in the PROC NLIN
statement. Because the weights change from iteration to iteration, it is not reasonable to expect the weighted residual sum of squares to decrease between iterations. The NOHALVE
option removes that restriction.
Examples where IRLS estimation is used include robust regression via M-estimation (Huber 1964, 1973), generalized linear models (McCullagh and Nelder 1989), and semivariogram fitting in spatial statistics (Schabenberger and Pierce 2002, Sect. 9.2). There are dedicated SAS/STAT procedures for robust regression (the ROBUSTREG procedure) and generalized linear models (the GENMOD and GLIMMIX procedures). Examples of weighted least squares fitting of a semivariogram function can be found in Chapter 122: The VARIOGRAM Procedure.
In this example we show an application of PROC NLIN for M-estimation only to illustrate the connection between robust regression and weighted least squares. The ROBUSTREG procedure is the appropriate tool to fit these models with SAS/STAT software.
M-estimation was introduced by Huber (1964, 1973) to estimate location parameters robustly. Beaton and Tukey (1974) applied the idea of M-estimation in regression models and introduced the biweight (or bisquare) weight function. See Holland and Welsch (1977) for this and other robust methods. Consider a linear regression model of the form
![\[ \mr{E}[Y_ i|x] = \mb{x}_ i’\bbeta + \epsilon _ i \]](images/statug_nlin0312.png)
In weighted least squares estimation you seek the parameters 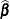 that minimize
that minimize
![\[ \sum _{i=1}^{n} w_ i \left( y_ i - \mb{x}_ i’\bbeta \right)^2 = \sum _{i=1}^{n} w_ i e_ i^2 \]](images/statug_nlin0313.png)
where 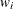 is the weight associated with the ith observation. The normal equations of this minimization problem can be written as
is the weight associated with the ith observation. The normal equations of this minimization problem can be written as
![\[ \sum _{i=1}^{n} w_ i e_ i \mb{x}_ i = \mb{0} \]](images/statug_nlin0315.png)
In M-estimation the corresponding equations take on the form
![\[ \sum _{i=1}^{n} \psi (e_ i) \mb{x}_ i = \mb{0} \]](images/statug_nlin0316.png)
where 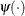 is a weighing function. The Beaton-Tukey biweight, for example, can be written as
is a weighing function. The Beaton-Tukey biweight, for example, can be written as
![\[ \psi (e_ i) = \left\{ \begin{array}{ll} e_ i \left( 1 - \left(\frac{e_ i}{\sigma k}\right)^2\right)^2 & |e_ i/\sigma | \leq k \cr 0 & |e_ i/\sigma | > k \end{array} \right. \]](images/statug_nlin0318.png)
Substitution into the estimating equation for M-estimation yields weighted least squares equations
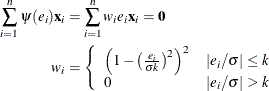
The biweight function involves two constants,  and k. The scale
and k. The scale  can be fixed or estimated from the fit in the previous iteration. If
can be fixed or estimated from the fit in the previous iteration. If  is estimated, a robust estimator of scale is typically used. In this example
is estimated, a robust estimator of scale is typically used. In this example  is fixed at 2. A common value for the constant k is k = 4.685.
is fixed at 2. A common value for the constant k is k = 4.685.
The following DATA step creates a SAS data set of the population of the United States (in millions), recorded at 10-year intervals starting in 1790 and ending in 1990. The aim is to fit a quadratic linear model to the population over time.
title 'U.S. Population Growth'; data uspop; input pop :6.3 @@; retain year 1780; year = year+10; yearsq = year*year; datalines; 3929 5308 7239 9638 12866 17069 23191 31443 39818 50155 62947 75994 91972 105710 122775 131669 151325 179323 203211 226542 248710 ;
The PROC NLIN code that follows fits this linear model by M-estimation and IRLS. The weight function is set to a zero or nonzero value depending on the value of the scaled residual. The NOHALVE option removes the requirement that the (weighted) residual sum of squares must decrease between iterations.
title 'Beaton/Tukey Biweight Robust Regression using IRLS'; proc nlin data=uspop nohalve; parms b0=20450.43 b1=-22.7806 b2=.0063456; model pop=b0+b1*year+b2*year*year; resid = pop-model.pop; sigma = 2; k = 4.685; if abs(resid/sigma)<=k then _weight_=(1-(resid / (sigma*k))**2)**2; else _weight_=0; output out=c r=rbi; run;
Parameter estimates from this fit are shown in Output 81.2.1, and the computed weights at the final iteration are displayed in Output 81.2.2. The observations for 1940 and 1950 are highly discounted because of their large residuals.
Output 81.2.1: Nonlinear Least-Squares Analysis
Output 81.2.2: Listing of Computed Weights from PROC NLIN
| Obs | pop | year | yearsq | rbi | sigma | k | _weight_ |
|---|---|---|---|---|---|---|---|
| 1 | 3.929 | 1790 | 3204100 | -0.93711 | 2 | 4.685 | 0.98010 |
| 2 | 5.308 | 1800 | 3240000 | 0.46091 | 2 | 4.685 | 0.99517 |
| 3 | 7.239 | 1810 | 3276100 | 1.11853 | 2 | 4.685 | 0.97170 |
| 4 | 9.638 | 1820 | 3312400 | 0.95176 | 2 | 4.685 | 0.97947 |
| 5 | 12.866 | 1830 | 3348900 | 0.32159 | 2 | 4.685 | 0.99765 |
| 6 | 17.069 | 1840 | 3385600 | -0.62597 | 2 | 4.685 | 0.99109 |
| 7 | 23.191 | 1850 | 3422500 | -0.94692 | 2 | 4.685 | 0.97968 |
| 8 | 31.443 | 1860 | 3459600 | -0.43027 | 2 | 4.685 | 0.99579 |
| 9 | 39.818 | 1870 | 3496900 | -1.08302 | 2 | 4.685 | 0.97346 |
| 10 | 50.155 | 1880 | 3534400 | -1.06615 | 2 | 4.685 | 0.97427 |
| 11 | 62.947 | 1890 | 3572100 | 0.11332 | 2 | 4.685 | 0.99971 |
| 12 | 75.994 | 1900 | 3610000 | 0.25539 | 2 | 4.685 | 0.99851 |
| 13 | 91.972 | 1910 | 3648100 | 2.03607 | 2 | 4.685 | 0.90779 |
| 14 | 105.710 | 1920 | 3686400 | 0.28436 | 2 | 4.685 | 0.99816 |
| 15 | 122.775 | 1930 | 3724900 | 0.56725 | 2 | 4.685 | 0.99268 |
| 16 | 131.669 | 1940 | 3763600 | -8.61325 | 2 | 4.685 | 0.02403 |
| 17 | 151.325 | 1950 | 3802500 | -8.32415 | 2 | 4.685 | 0.04443 |
| 18 | 179.323 | 1960 | 3841600 | -0.98543 | 2 | 4.685 | 0.97800 |
| 19 | 203.211 | 1970 | 3880900 | 0.95088 | 2 | 4.685 | 0.97951 |
| 20 | 226.542 | 1980 | 3920400 | 1.03780 | 2 | 4.685 | 0.97562 |
| 21 | 248.710 | 1990 | 3960100 | -1.33067 | 2 | 4.685 | 0.96007 |
You can obtain this analysis more conveniently with PROC ROBUSTREG. The procedure re-estimates the scale parameter robustly between iterations. To obtain an analysis with a fixed scale parameter as in this example, use the following PROC ROBUSTREG statements:
proc robustreg data=uspop method=m(scale=2); model pop = year year*year; output out=weights weight=w; run; proc print data=weights; run;
Note that the computation of standard errors in the ROBUSTREG procedure is different from the calculations in the NLIN procedure.