The IRT Procedure

Model and Item Fit

The IRT procedure includes five model fit statistics: log likelihood, Akaike’s information criterion (AIC), Bayesian information criterion (BIC), likelihood ratio chi-square 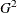$G^2$ , and Pearson’s chi-square.

The following two equations compute the likelihood ratio chi-square 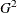$G^2$ and Pearson’s chi-square,

$G^2 = 2\left[\sum _{l=1}^{L} r_ l \log \frac{r_ l}{N P_ l}\right]$

$\chi ^2 = \sum _{l=1}^{L} \frac{(r_ l-NP_ l)^2}{N P_ l}$

where N is the number of subjects, L is number of possible response patterns, 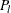$P_ l$ is the estimated probability of observing response pattern l, and 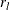$r_ l$ is the number of subjects who have response pattern l. If the model is true, these two statistics asymptotically follow central chi-square distribution with degrees of freedom 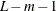$L-m-1$ , where m is the number of free parameters in the model. When L (the number of possible response patterns) is much greater than N, the frequency table is sparse. This invalidates the use of chi-square distribution as the asymptotic distribution for these two statistics, and as a result the likelihood ratio chi-square and Pearson’s chi-square statistics should not be used to evaluate overall model fit.

For item fit, PROC IRT computes the likelihood ratio 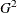$G^2$ and Pearson’s chi-square. Pearson’s chi-square statistic, proposed by Yen (1981), has the form

$Q_{1j} = \sum _{k=1}^{10} N_ k\frac{(O_{jk} - E_{jk})^2}{E_{jk}(1-E_{jk})}$

The likelihood ratio 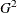$G^2$ , proposed by McKinley and Mills (1985), uses the following equation:

$G^2 = 2 \sum _{k=1}^{10} N_ k \left[ O_{jk} \log \frac{O_{jk}}{E_{ik}} + (1-O_{jk})\log \frac{1-O_{jk}}{1-E_{ik}}\right]$

These two statistics approximately follow a central chi-square distribution with 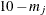$10-m_ j$ degrees of freedom, where 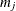$m_ j$ is the number of free parameters for item j.

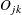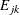To calculate these two statistics, first order all the subjects according to their estimated factor scores, and then partition them into 10 intervals such that the number of subjects in each interval is approximately equal. $O_{jk}$ and $E_{jk}$ are the observed proportion and expected proportion, respectively, of subjects in interval k who have a correct response on item j. The expected proportions 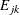$E_{jk}$ are computed as the mean predicted probability of a correct response in interval k.