The HPSPLIT Procedure
Variable Importance
A training data set can contain a large number of predictors. Some predictors are useful for predicting the response variable, and others are not. You can use the HPSPLIT procedure to select the most useful predictors based on variable importance. (See Example 61.5: Assessing Variable Importance.) Variable importance is an indication of which predictors are most useful for predicting the response variable. Various measures of variable importance have been proposed in the data mining literature.
The most important variables might not be the ones near the top of the tree. PROC HPSPLIT measures variable importance based on the following metrics: count, surrogate count, RSS, and relative importance. The count-based variable importance simply counts the number of times in the tree that a particular variable is used in a split. Similarly, the surrogate count tallies the number of times that a variable is used in a surrogate splitting rule.
The RSS-based metric measures variable importance based on the change of RSS when a split is found at a node. The change is
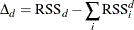
where
-
d denotes the node
-
i denotes the index of a child that this node has
-
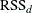 is the RSS if the node is treated as a leaf
is the RSS if the node is treated as a leaf
-
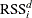 is the RSS of the node after it has been split
is the RSS of the node after it has been split
If the change in RSS is negative (which is possible when you use the validation set), then the change is set to 0.
If surrogate rules are in effect, they are also credited with a portion of the change in RSS. The credit is proportional to
the agreement between the primary and surrogate splitting rules at the node. The agreement at node d, 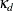 , is defined as
, is defined as
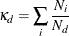
where
-
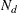 is the number of nonmissing observations
is the number of nonmissing observations
-
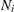 is the number of observations that were assigned to i by both the primary and surrogate rules
is the number of observations that were assigned to i by both the primary and surrogate rules
The change in RSS from the surrogate rules is defined as
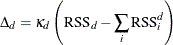
The RSS-based importance is then defined as

where D is the total number of nodes.
The relative importance metric is a number between 0 and 1. It is calculated in two steps. First, PROC HPSPLIT finds the maximum RSS-based variable importance. Then, for each variable, it calculates the relative variable importance as the RSS-based importance of this variable divided by the maximum RSS-based importance among all the variables.
The RSS and relative importance are calculated from the training set. They are calculated again from the validation set if one exists.
