The NLMIXED Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 Modeling Assumptions and Notation Integral Approximations Built-in Log-Likelihood Functions Optimization Algorithms Finite-Difference Approximations of Derivatives Hessian Scaling Active Set Methods Line-Search Methods Restricting the Step Length Computational Problems Covariance Matrix Prediction Computational Resources Displayed Output ODS Table Names
Modeling Assumptions and Notation Integral Approximations Built-in Log-Likelihood Functions Optimization Algorithms Finite-Difference Approximations of Derivatives Hessian Scaling Active Set Methods Line-Search Methods Restricting the Step Length Computational Problems Covariance Matrix Prediction Computational Resources Displayed Output ODS Table Names -
Examples

- References
Example 63.4 Poisson-Normal Model with Count Data
This example uses the pump failure data of Gaver and O’Muircheartaigh (1987). The number of failures and the time of operation are recorded for 10 pumps. Each of the pumps is classified into one of two groups corresponding to either continuous or intermittent operation. The data are as follows:
data pump; input y t group; pump = _n_; logtstd = log(t) - 2.4564900; datalines; 5 94.320 1 1 15.720 2 5 62.880 1 14 125.760 1 3 5.240 2 19 31.440 1 1 1.048 2 1 1.048 2 4 2.096 2 22 10.480 2 ;
Each row denotes data for a single pump, and the variable logtstd contains the centered operation times.
Letting 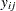 denote the number of failures for the
denote the number of failures for the  th pump in the
th pump in the 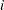 th group, Draper (1996) considers the following hierarchical model for these data:
th group, Draper (1996) considers the following hierarchical model for these data:
 |
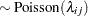 |
|||
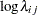 |
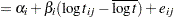 |
|||
 |
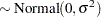 |
The model specifies different intercepts and slopes for each group, and the random effect is a mechanism for accounting for overdispersion.
The corresponding PROC NLMIXED statements are as follows:
proc nlmixed data=pump; parms logsig 0 beta1 1 beta2 1 alpha1 1 alpha2 1; if (group = 1) then eta = alpha1 + beta1*logtstd + e; else eta = alpha2 + beta2*logtstd + e; lambda = exp(eta); model y ~ poisson(lambda); random e ~ normal(0,exp(2*logsig)) subject=pump; estimate 'alpha1-alpha2' alpha1-alpha2; estimate 'beta1-beta2' beta1-beta2; run;
The selected output is as follows.
| Dimensions | |
|---|---|
| Observations Used | 10 |
| Observations Not Used | 0 |
| Total Observations | 10 |
| Subjects | 10 |
| Max Obs Per Subject | 1 |
| Parameters | 5 |
| Quadrature Points | 5 |
The "Dimensions" table indicates that data for 10 pumps are used with one observation for each (Output 63.4.1).
| Iteration History | ||||||
|---|---|---|---|---|---|---|
| Iter | Calls | NegLogLike | Diff | MaxGrad | Slope | |
| 1 | 2 | 30.6986932 | 2.162768 | 5.107253 | -91.602 | |
| 2 | 5 | 30.0255468 | 0.673146 | 2.761738 | -11.0489 | |
| 3 | 7 | 29.726325 | 0.299222 | 2.990401 | -2.36048 | |
| 4 | 9 | 28.7390263 | 0.987299 | 2.074431 | -3.93678 | |
| 5 | 10 | 28.3161933 | 0.422833 | 0.612531 | -0.63084 | |
| 6 | 12 | 28.09564 | 0.220553 | 0.462162 | -0.52684 | |
| 7 | 14 | 28.0438024 | 0.051838 | 0.405047 | -0.10018 | |
| 8 | 16 | 28.0357134 | 0.008089 | 0.135059 | -0.01875 | |
| 9 | 18 | 28.033925 | 0.001788 | 0.026279 | -0.00514 | |
| 10 | 20 | 28.0338744 | 0.000051 | 0.00402 | -0.00012 | |
| 11 | 22 | 28.0338727 | 1.681E-6 | 0.002864 | -5.09E-6 | |
| 12 | 24 | 28.0338724 | 3.199E-7 | 0.000147 | -6.87E-7 | |
| 13 | 26 | 28.0338724 | 2.532E-9 | 0.000017 | -5.75E-9 | |
| NOTE: GCONV convergence criterion satisfied. |
The "Iteration History" table indicates successful convergence in 13 iterations (Output 63.4.2).
| Fit Statistics | |
|---|---|
| -2 Log Likelihood | 56.1 |
| AIC (smaller is better) | 66.1 |
| AICC (smaller is better) | 81.1 |
| BIC (smaller is better) | 67.6 |
The "Fit Statistics" table lists the final log likelihood and associated information criteria (Output 63.4.3).
| Parameter Estimates | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | Estimate | Standard Error | DF | t Value | Pr > |t| | Alpha | Lower | Upper | Gradient |
| logsig | -0.3161 | 0.3213 | 9 | -0.98 | 0.3508 | 0.05 | -1.0429 | 0.4107 | -0.00002 |
| beta1 | -0.4256 | 0.7473 | 9 | -0.57 | 0.5829 | 0.05 | -2.1162 | 1.2649 | -0.00002 |
| beta2 | 0.6097 | 0.3814 | 9 | 1.60 | 0.1443 | 0.05 | -0.2530 | 1.4724 | -1.61E-6 |
| alpha1 | 2.9644 | 1.3826 | 9 | 2.14 | 0.0606 | 0.05 | -0.1632 | 6.0921 | -5.25E-6 |
| alpha2 | 1.7992 | 0.5492 | 9 | 3.28 | 0.0096 | 0.05 | 0.5568 | 3.0415 | -5.73E-6 |
| Additional Estimates | ||||||||
|---|---|---|---|---|---|---|---|---|
| Label | Estimate | Standard Error | DF | t Value | Pr > |t| | Alpha | Lower | Upper |
| alpha1-alpha2 | 1.1653 | 1.4855 | 9 | 0.78 | 0.4529 | 0.05 | -2.1952 | 4.5257 |
| beta1-beta2 | -1.0354 | 0.8389 | 9 | -1.23 | 0.2484 | 0.05 | -2.9331 | 0.8623 |
The "Parameter Estimates" and "Additional Estimates" tables list the maximum likelihood estimates for each of the parameters and two differences (Output 63.4.4). The point estimates for the mean parameters agree fairly closely with the Bayesian posterior means reported by Draper (1996); however, the likelihood-based standard errors are roughly half the Bayesian posterior standard deviations. This is most likely due to the fact that the Bayesian standard deviations account for the uncertainty in estimating 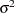 , whereas the likelihood values plug in its estimated value. This downward bias can be corrected somewhat by using the
, whereas the likelihood values plug in its estimated value. This downward bias can be corrected somewhat by using the 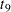 distribution shown here.
distribution shown here.