The NLMIXED Procedure
-
Overview
-
Getting Started
-
Syntax
-
Details
Modeling Assumptions and Notation Integral Approximations Built-in Log-Likelihood Functions Optimization Algorithms Finite-Difference Approximations of Derivatives Hessian Scaling Active Set Methods Line-Search Methods Restricting the Step Length Computational Problems Covariance Matrix Prediction Computational Resources Displayed Output ODS Table Names
-
Examples
- References
| Finite-Difference Approximations of Derivatives |
The FD= and FDHESSIAN= options specify the use of finite-difference approximations of the derivatives. The FD= option specifies that all derivatives are approximated using function evaluations, and the FDHESSIAN= option specifies that second-order derivatives are approximated using gradient evaluations.
Computing derivatives by finite-difference approximations can be very time-consuming, especially for second-order derivatives based only on values of the objective function (FD= option). If analytical derivatives are difficult to obtain (for example, if a function is computed by an iterative process), you might consider one of the optimization techniques that use first-order derivatives only (QUANEW, DBLDOG, or CONGRA). In the expressions that follow, 
denotes the parameter vector, 
denotes the step size for the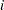 
th parameter, and 
is a vector of zeros with a 
in the 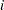th position.
Forward-Difference Approximations
The forward-difference derivative approximations consume less computer time, but they are usually not as precise as approximations that use central-difference formulas.
-
For first-order derivatives,
additional function calls are required: 
-
For second-order derivatives based on function calls only (Dennis and Schnabel 1983, p. 80),
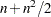additional function calls are required for dense Hessian: 
-
For second-order derivatives based on gradient calls (Dennis and Schnabel 1983, p. 103),
additional gradient calls are required: 
Central-Difference Approximations
Central-difference approximations are usually more precise, but they consume more computer time than approximations that use forward-difference derivative formulas.
-
For first-order derivatives,
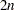additional function calls are required: 
-
For second-order derivatives based on function calls only (Abramowitz and Stegun 1972, p. 884),
additional function calls are required. 
-
For second-order derivatives based on gradient calls,
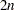additional gradient calls are required: 
You can use the FDIGITS= option to specify the number of accurate digits in the evaluation of the objective function. This specification is helpful in determining an appropriate interval size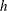 
to be used in the finite-difference formulas.
The step sizes 
, 
are defined as follows:
For the forward-difference approximation of first-order derivatives that use function calls and second-order derivatives that use gradient calls,
. For the forward-difference approximation of second-order derivatives that use only function calls and all central-difference formulas,
.
The value of 
is defined by the FDIGITS= option:
, 
. 
.