The NLMIXED Procedure

In each iteration 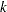, the (dual) quasi-Newton, conjugate gradient, and Newton-Raphson minimization techniques use iterative line-search algorithms that try to optimize a linear, quadratic, or cubic approximation of 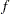along a feasible descent search direction ,

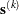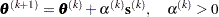by computing an approximately optimal scalar .

Therefore, a line-search algorithm is an iterative process that optimizes a nonlinear function of one parameter () within each iteration 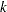of the optimization technique. Since the outside iteration process is based only on the approximation of the objective function, the inside iteration of the line-search algorithm does not have to be perfect. Usually, it is satisfactory that the choice of significantly reduces (in a minimization) the objective function. Criteria often used for termination of line-search algorithms are the Goldstein conditions (see Fletcher 1987).

You can select various line-search algorithms by specifying the LINESEARCH= option. The line-search method LINESEARCH=2 seems to be superior when function evaluation consumes significantly less computation time than gradient evaluation. Therefore, LINESEARCH=2 is the default method for Newton-Raphson, (dual) quasi-Newton, and conjugate gradient optimizations.

You can modify the line-search methods LINESEARCH=2 and LINESEARCH=3 to be exact line searches by using the LSPRECISION= option and specifying the parameter described in Fletcher (1987). The line-search methods LINESEARCH=1, LINESEARCH=2, and LINESEARCH=3 satisfy the left-side and right-side Goldstein conditions (see Fletcher 1987). When derivatives are available, the line-search methods LINESEARCH=6, LINESEARCH=7, and LINESEARCH=8 try to satisfy the right-side Goldstein condition; if derivatives are not available, these line-search algorithms use only function calls.