The GAMPL Procedure

MODEL Statement

Subsections:

Response Variable Options
Spline Options
Model Options

MODEL response <(response-options)> = <PARAM(effects)> <spline-effects> </ model-options>;

MODEL events / trials = <PARAM(effects)> <spline-effects> </ model-options>;

The MODEL statement specifies the response (dependent or target) variable and the predictor (independent or explanatory) effects of the model. You can specify the response in the form of a single variable or in the form of a ratio of two variables, which are denoted events/trials. The first form applies to all distribution families; the second form applies only to summarized binomial response data. When you have binomial data, the events variable contains the number of positive responses (or events) and the trials variable contains the number of trials. The values of both events and (trials – events) must be nonnegative, and the value of trials must be positive. If you specify a single response variable that is in a CLASS statement, then the response is assumed to be binary.

You can specify parametric effects that are constructed from variables in the input data set and include the effects in the parentheses of a PARAM( ) option, which can appear multiple times. For information about constructing the model effects, see the section Specification and Parameterization of Model Effects.

You can specify spline-effects by including independent variables inside the parentheses of the SPLINE( ) option. Only continuous variables (not classification variables) can be specified in spline-effects. Each spline-effect can have at least one variable and optionally some spline-options . You can specify any number of spline-effects. The following table shows some examples.

Table 7.3: continued

Spline Effect Specification	Meaning
`Spline(x)`	Constructs the univariate spline with `x` and uses the observed data points as knots. The maximum degrees of freedom is 10. PROC GAMPL uses an optimization algorithm to determine the optimal smoothing parameter.
`Spline(x1/knots=list(1 to 10))`	Constructs the univariate spline by using `x1` and a supplied list of knots from 1 to 10. PROC GAMPL uses an optimization algorithm to determine the optimal smoothing parameter.
`Spline(x2 x3/smooth=0.3)`	Constructs the bivariate spline by using `x2` and `x3` and a fixed smoothing parameter 0.3.
`Spline(x4 x5 x6/maxdf=40)`	Constructs the trivariate spline by using `x4`, `x5`, and `x6` and a maximum of 40 degrees of freedom. PROC GAMPL uses an optimization algorithm to determine the optimal smoothing parameter.

Both parametric effects and spline effects are optional. If none are specified, a model that contains only an intercept is fitted. If only parametric effects are present, PROC GAMPL fits a parametric generalized linear model by using the terms inside the parentheses of all PARAM( ) terms. If only spline effects are present, PROC GAMPL fits a nonparametric additive model. If both types of effects are present, PROC GAMPL fits a semiparametric model by using the parametric effects as the linear part of the model.

There are three sets of options in the MODEL statement. The response-options determine how the GAMPL procedure models probabilities for binary data. The spline-options controls how each spline term forms basis expansions. The model-options control other aspects of model formation and inference. Table 7.4 summarizes these options.

Table 7.4: MODEL Statement Options

Option	Description
Response Variable Options for Binary Models
DESCENDING	Reverses the response categories
EVENT=	Specifies the event category
ORDER=	Specifies the sort order
REF=	Specifies the reference category
Smoothing Options for Spline Effects
DETAILS	Requests detailed spline information
DF=	Specifies the fixed degrees of freedom
INITSMOOTH=	Specifies the starting value for the smoothing parameter
KNOTS=	Specifies the knots to be used for constructing the spline
M=	Specifies polynomial orders for constructing the spline
MAXDF=	Specifies the maximum degrees of freedom
MAXKNOTS=	Specifies the maximum number of knots to be used for constructing the spline
MAXSMOOTH=	Specifies the upper bound for the smoothing parameter
MINSMOOTH=	Specifies the lower bound for the smoothing parameter
SMOOTH=	Specifies a fixed smoothing parameter
Model Options
ALLOBS	Requests all nonmissing values of spline variables for constructing spline basis functions regardless of other model variables
CRITERION=	Specifies the model evaluation criterion
DISPERSION \| PHI=	Specifies the fixed dispersion parameter
DISTRIBUTION \| DIST=	Specifies the response distribution
FDHESSIAN	Requests a finite-difference Hessian for smoothing parameter selection
INITIALPHI=	Specifies the starting value of the dispersion parameter
LINK=	Specifies the link function
NORMALIZE	Requests normalized spline basis functions for model fitting
MAXPHI=	Specifies the upper bound for searching the dispersion parameter
METHOD=	Specifies the algorithm for selecting smoothing parameters
MINPHI=	Specifies the lower bound for searching the dispersion parameter
OFFSET=	Specifies the offset variable
RIDGE=	Specifies the ridge parameter
SCALE=	Specifies the method for estimating the dispersion parameter

Response Variable Options

Response variable options determine how the GAMPL procedure models probabilities for binary data.

You can specify the following response-options by enclosing them in parentheses after the response variable.

DESCENDING DESC

reverses the order of the response categories. If you specify both the DESCENDING and ORDER= options, PROC GAMPL orders the response categories according to the ORDER= option and then reverses that order.

EVENT=‘category’ | FIRST | LAST

specifies the event category for the binary response model. PROC GAMPL models the probability of the event category. The EVENT= option has no effect when there are more than two response categories.

You can specify any of the following:

‘category’

specifies that observations whose value matches category (formatted, if a format is applied) in quotation marks represent events in the data. For example, the following statements specify that observations that have a formatted value of '1' represent events in the data. The probability that is modeled by the GAMPL procedure is thus the probability that the variable def takes on the (formatted) value '1'.

    proc gampl data=MyData;
       class A B C;
       model def(event ='1') = param(A B C) spline(x1 x2 x3);
    run;

FIRST

designates the first ordered category as the event.

LAST

designates the last ordered category as the event.

By default, EVENT=FIRST.

specifies the sort order for the levels of the response variable. When ORDER=FORMATTED (the default) for numeric variables for which you have supplied no explicit format (that is, for which there is no corresponding FORMAT statement in the current PROC GAMPL run or in the DATA step that created the data set), the levels are ordered by their internal (numeric) value. Table 7.5 shows the interpretation of the ORDER= option.

Table 7.5: Sort Order

ORDER=	Levels Sorted By
DATA	Order of appearance in the input data set
FORMATTED	External formatted value, except for numeric variables that have no explicit format, which are sorted by their unformatted (internal) value
FREQ	Descending frequency count (levels that have the most observations come first in the order)
FREQDATA	Order of descending frequency count; within counts by order of appearance in the input data set when counts are tied
FREQFORMATTED	Order of descending frequency count; within counts by formatted value when counts are tied
FREQINTERNAL	Order of descending frequency count; within counts by unformatted value when counts are tied
INTERNAL	Unformatted value

By default, ORDER=FORMATTED. For the FORMATTED and INTERNAL orders, the sort order is machine-dependent.

For more information about sort order, see the chapter about the SORT procedure in Base SAS Procedures Guide and the discussion of BY-group processing in SAS Language Reference: Concepts.

REF=‘category’ | FIRST | LAST

specifies the reference category for the binary response model. Specifying one response category as the reference is the same as specifying the other response category as the event category. You can specify any of the following:

‘category’: specifies that observations whose value matches category (formatted, if a format is applied) are designated as the reference.
FIRST: designates the first ordered category as the reference
LAST: designates the last ordered category as the reference.

By default, REF=LAST.

Spline Options

DETAILS

requests a detailed spline specification information table.

DF=number

specifies a fixed degrees of freedom. When you specify this option, no smoothing parameter selection is performed on the spline term. If number is not an integer, then number is truncated to an integer.

INITSMOOTH=number

specifies the starting value for a smoothing parameter. The number must be nonnegative.

KNOTS=method

specifies the method for supplying user-defined knot values instead of using data values for constructing basis expansions. You can use the following methods for supplying the knots:

LIST(list-of-values)

specifies a list of values as knots for the spline construction. For a multivariate spline term, the listed values are taken as multiple row vectors, where each vector has values that are ordered by specified variables. If the last row vector of knots contains fewer values than the number of variables, then the last row vector is ignored. For example, the following specification of a spline term produces two actual knot vectors ( $\bm {k}_1$ and $\bm {k}_2$ ) and the value 5 is ignored.

spline(x1 x2/knots=list(1 2 3 4 5))

Table 7.6: Knot Values for a Bivariate Spline with a Supplied List

	`x1`	`x2`
$\bm {k}_1$	1	2
$\bm {k}_2$	3	4

EQUAL(n)

specifies the number of equally spaced interior knots for every variable in a spline term. Two boundary knots are automatically added to the knot list for each variable such that the total number of knots is $(n+2)^ d$ , where d is the number of variables in the spline term. For a multivariate spline term, knot values for each variable are determined independently from the corresponding boundary values. For example, if the boundary points for x1 are 1 and 5 and the boundary points for x2 are 2 and 6, then the following specification of a spline term produces nine actual knots ( $\bm {k}_1$ — $\bm {k}_9$ ), which consist of two boundary knots and one interior knot for each variable.

spline(x1 x2/knots=equal(1))

Table 7.7: Knot Values for a Bivariate Spline with One Interior Knot

	`x1`	`x2`
$\bm {k}_1$	1	2
$\bm {k}_2$	1	4
$\bm {k}_3$	1	6
$\bm {k}_4$	3	2
$\bm {k}_5$	3	4
$\bm {k}_6$	3	6
$\bm {k}_7$	5	2
$\bm {k}_8$	5	4
$\bm {k}_9$	5	6

M=number

specifies the order of the derivative in the penalty term. The number must be a positive integer. The default is $\max (2,\mathrm{int}(d/2)+1)$ , where d is the number of variables in the spline term.

MAXDF=number

specifies the maximum number of degrees of freedom. When a thin-plate regression spline is formed, the specified number is used for constructing a low-rank penalty matrix to approximate the penalty matrix via the truncated eigendecomposition. The number must be greater than ${m+d-1\choose d}$ , where m is the derivative order that is specified in the M= option. The default is $10\times d$ . For more information, see the section Thin-Plate Regression Splines.

MAXKNOTS=number

specifies the maximum number of knots if data points are used to form knots. If KNOTS=LIST(list-of-values) is not specified, PROC GAMPL forms knots from unique data points. If the number of unique data points is greater than number, a subset of size number is formed by random sampling from all unique data points. The number cannot exceed the largest integer that can be stored on the given machine. By default, MAXKNOTS=2000.

MAXSMOOTH=number

specifies the upper bound for the smoothing parameter. The default is the largest double-precision value.

MINSMOOTH=number

specifies the lower bound for the smoothing parameter. By default, MINSMOOTH=0.

SMOOTH=number

specifies a fixed smoothing parameter. When you specify this option, no smoothing parameter selection is performed on the spline term.

Model Options

ALLOBS

requests that all nonmissing values of the variables be specified in a spline term for constructing the spline basis functions, regardless of whether other model variables are missing.

CRITERION=criterion

specifies the model evaluation criterion for selecting smoothing parameters for spline-effects. You can specify the following values:

GACV<(FACTOR=number | GAMMA=number)>: uses the generalized approximate cross validation (GACV) criterion to evaluate models.
GCV<(FACTOR=number | GAMMA=number)>: uses the generalized cross validation (GCV) criterion to evaluate models.
UBRE<(FACTOR=number | GAMMA=number)>: uses the unbiased risk estimator (UBRE) criterion to evaluate models.

The default criterion depends on the value of the DISTRIBUTION= option. For distributions that involve dispersion parameters, GCV is the default. For distributions without dispersion parameters, UBRE is the default. For all three criteria, you can optionally use the FACTOR= option to specify an extra tuning parameter in order to penalize more for model roughness. The value of number must be greater than or equal to 1. For more information about the model evaluation criteria, see Model Evaluation Criteria.

DISPERSION=number

specifies a fixed dispersion parameter for distributions that have a dispersion parameter. The dispersion parameter that is used in all computations is fixed at number; it is not estimated.

DISTRIBUTION=keyword

specifies the response distribution for the model. The keywords and their associated distributions are shown in Table 7.8.

Table 7.8: Built-In Distribution Functions

	Distribution
DISTRIBUTION=	Function
BINARY	Binary
BINOMIAL	Binary or binomial
GAMMA	Gamma
INVERSEGAUSSIAN \| IG	Inverse Gaussian
NEGATIVEBINOMIAL \| NB	Negative binomial
NORMAL \| GAUSSIAN	Normal
POISSON	Poisson

If you do not specify a link function in the LINK= option, a default link function is used. The default link function for each distribution is shown in Table 7.9. You can use any link function shown in Table 7.10 by specifying the LINK= option. Other commonly used link functions for each distribution are shown in Table 7.9.

Table 7.9: Default and Commonly Used Link Functions

	Default	Other Commonly Used
DISTRIBUTION=	Link Function	Link Functions
BINARY	Logit	Probit, complementary log-log, log-log
BINOMIAL	Logit	Probit, complementary log-log, log-log
GAMMA	Reciprocal	Log
INVERSEGAUSSIAN \| IG	Reciprocal square	Log
NEGATIVEBINOMIAL \| NB	Log
NORMAL \| GAUSSIAN	Identity	Log
POISSON	Log

FDHESSIAN

requests that the second-order derivatives (Hessian) be computed using finite-difference approximations based on evaluation of the first-order derivatives (gradient). This option might be useful if the analytical Hessian takes a long time to compute.

INITIALPHI=number

specifies a starting value for iterative maximum likelihood estimation of the dispersion parameter for distributions that have a dispersion parameter.

LINK=keyword

specifies the link function for the model. The keywords and the associated link functions are shown in Table 7.10. Default and commonly used link functions for the available distributions are shown in Table 7.9.

Table 7.10: Built-In Link Functions

	Link
LINK=	Function	$g(\mu ) =\eta =$
CLOGLOG \| CLL	Complementary log-log	$\log (-\log (1-\mu ))$
IDENTITY \| ID	Identity	$\mu$
INV \| RECIP	Reciprocal	$1/\mu$
INV2	Reciprocal square	$1/\mu ^2$
LOG	Logarithm	$\log (\mu )$
LOGIT	Logit	$\log (\mu /(1-\mu ))$
LOGLOG	Log-log	$-\log (-\log (\mu ))$
PROBIT	Probit	$\Phi ^{-1}(\mu )$

$\Phi ^{-1}(\cdot )$ denotes the quantile function of the standard normal distribution.

MAXPHI=number

specifies an upper bound for maximum likelihood estimation of the dispersion parameter for distributions that have a dispersion parameter.

METHOD=OUTER | PERFORMANCE

specifies the algorithm for selecting smoothing parameters for spline-effects. You can specify the following values:

OUTER

specifies the outer iteration method for selecting smoothing parameters. For more information about the method, see the section Outer Iteration.

Note: The outer iteration method is experimental in this release.

PERFORMANCE

specifies the performance iteration method for selecting smoothing parameters. For more information about the method, see the section Performance Iteration.

By default, METHOD=PERFORMANCE.

MINPHI=number

specifies a lower bound for maximum likelihood estimation of the dispersion parameter for distributions that have a dispersion parameter.

NORMALIZE

requests normalized spline basis functions for model fitting. After the regression spline basis functions are computed, each column is standardized to have a unit standard error. The corresponding penalty matrix is also scaled accordingly. This option might be helpful when you have badly scaled data.

OFFSET=variable

specifies a variable to be used as an offset to the linear predictor. An offset plays the role of an effect whose coefficient is known to be 1. The offset variable cannot appear in the CLASS statement or elsewhere in the MODEL statement. Observations that have missing values for the offset variable are excluded from the analysis.

RIDGE=number

allows a ridge parameter such that a diagonal matrix $\bH : \bH _{ii}=$ number is added to the optimization problem with respect to regression parameters:

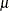
$\min (\mb{y}-\bX \bbeta )’(\mb{y}-\bX \bbeta )+\bbeta ’\bS _{\blambda }\bbeta +\bbeta ’\bH \bbeta \quad \text {with respect to}\quad \bbeta$

By default, RIDGE=0. Specifying a small ridge parameter might be helpful if the model matrix $\bX ’\bX +\bS _{\blambda }$ is close to singular.

SCALE=DEVIANCE | MLE | PEARSON

specifies the method for estimating the scale and dispersion parameters. You can specify the following values:

DEVIANCE: estimates the dispersion parameter by using the deviance statistic.
MLE: computes the dispersion parameter by maximizing the likelihood or penalized likelihood.
PEARSON: estimates the dispersion parameter by using Pearson’s statistic.

By default, SCALE=MLE.