The GAMPL Procedure

Degrees of Freedom

Let $\bW $ be the adjusted weight matrix at convergence, and let 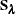$\bS _{\blambda }$ be the roughness penalty matrix with selected smoothing parameters. The degrees of freedom matrix is defined as in Wood (2006):

\[ \bF = (\bX ’\bW \bX +\bS _{\blambda })^{-1}\bX ’\bW \bX \]

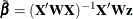Given the adjusted response $\mb{z}$, the parameter estimate is shown to be $\tilde{\bbeta }=(\bX ’\bW \bX )^{-1}\bX ’\bW \mb{z}$ for the model without penalization, and the parameter estimate is 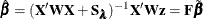$\hat{\bbeta }=(\bX ’\bW \bX +\bS _{\blambda })^{-1}\bX ’\bW \mb{z}=\bF \tilde{\bbeta }$ with penalization. 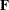$\bF $ is thus the matrix that projects or maps the unpenalized parameter estimates to the penalized ones.

The model degrees of freedom is given as

\[ \mathrm{df} = \mathrm{tr}(\bF ) \]

And the degrees of freedom for error is given as

\[ \mathrm{df}_ r = n - 2\mathrm{df} + \mathrm{tr}(\bF \bF ) \]

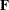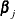For the jth spline term, the degrees of freedom for the component is defined to be the trace of the submatrix of $\bF $ that corresponds to parameter estimates $\bbeta _ j$:

\[ \mathrm{df}_ j = \mathrm{tr}(\bF _ j) \]

The degrees of freedom for the smoothing component test of the jth term is defined similarly as

\[ \mathrm{df}_ j^ t = 2\mathrm{df}_ j-\mathrm{tr}((\bF \bF )_ j) \]