The GAMPL Procedure

Generalized Additive Models

Subsections:

Generalized Linear Models

All probability distributions that the GAMPL procedure fits are members of an exponential family of distributions. For the specification of an exponential family, see the section "Generalized Linear Models Theory" in Chapter 44: The GENMOD Procedure in SAS/STAT 14.1 User's Guide.

Table 7.11 lists and defines some common notation that is used in the context of generalized linear models and generalized additive models.

Table 7.11: Common Notation

Notation

Meaning

$\ell $

Log-likelihood

$\ell _ p $

Penalized log-likelihood

$D $

Deviance

$D_ p $

Penalized deviance

$g $

Link function

$g^{-1} $

Inverse link function

$\bmu $

Response mean $\bmu =g^{-1}(\bm {\eta })$

$\bm {\eta }$

Linear predictor $\bm {\eta }=\bX \bbeta $

$\phi $

Dispersion parameter

$\mb{z} $

Column of adjusted response variable

$\bnu $

Column of response variance

$\omega _ i $

Prior weight for each observation

$w_ i $

Adjusted weight for each observation

$\mb{W} $

Diagonal matrix of adjusted weights


The GAMPL procedure supports the following distributions: binary, binomial, gamma, inverse Gaussian, negative binomial, normal (Gaussian), and Poisson.

For forms of log-likelihood functions for each of the probability distributions, see the section "Log-Likelihood Functions" in Chapter 44: The GENMOD Procedure in SAS/STAT 14.1 User's Guide. For forms of the deviance for each of the probability distributions, see the section "Goodness of Fit" in Chapter 44: The GENMOD Procedure in SAS/STAT 14.1 User's Guide.

Generalized Additive Models

Generalized additive models are extensions of generalized linear models (Nelder and Wedderburn 1972). For each observation that has a response $Y_ i$ and a row vector of the model matrix $\mb{x}_ i$, both generalized additive models and generalized linear models assume the model additivity

\[ g(\mu _ i) = f_1(\mb{x}_{i1}) + \dots + f_ p(\mb{x}_{ip}) \]

where $\mu _ i=E(Y_ i)$ and $Y_ i$ is independently distributed in some exponential family. Generalized linear models further assume model linearity by $f_ j(\mb{x}_{ij})=\mb{x}_{ij}\beta _ j$ for $j=1,\dots ,p$. Generalized additive models relax the linearity assumption by allowing some smoothing functions $f_ j$ to characterize the dependency. The GAMPL procedure constructs the smoothing functions by using thin-plate regression splines. For more information about generalized additive models and other type of smoothing functions, see Chapter 41: The GAM Procedure in SAS/STAT 14.1 User's Guide.

Consider a generalized additive model that has some linear terms $\bX _ L$ with coefficients $\bbeta _ L$ and p smoothing functions $f_ j$. Each smoothing function can be constructed by thin-plate regression splines with a smoothing parameter $\lambda _ j$. Using the notations described in the section Low-Rank Approximation, you can characterize each smoothing function by

\[ \bbeta _ j = \left[\begin{matrix} \btheta _ j \\ \tilde{\bdelta }_ j \end{matrix}\right], \quad \bX _ j = [\bT _ j : \bU _{kj}\bD _{kj}\bZ _ j ], \quad \text {and} \quad \bS _ j = \left[\begin{matrix} \mb{0} & \mb{0} \\ \mb{0} & \bZ _ j’\bD _{kj} \bZ _ j \end{matrix}\right] \]

Notice that each smoothing function representation contains a zero-degree polynomial that corresponds to a constant. Having multiple constant terms makes the smoothing functions unidentifiable. The solution is to include a global constant term (that is, the intercept) in the model and enforce the centering constraint to each smoothing function. You can write the constraint as

\[ \mb{1}’\bX _ j\bbeta _ j = 0 \]

By using a similar approach as the linear constraint for thin-plate regression splines, you obtain the orthogonal column basis 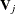$\bV _ j$ via the QR decomposition of $\bX _ j’\mb{1}$ such that $\mb{1}’\bX _ j\bV _ j=0$. Each smoothing function can be reparameterized as $\tilde{\bX }_ j=\bX _ j\bV _ j$.

Let $\bX = [ \bX _ L : \tilde{\bX }_1 : \dots : \tilde{\bX }_ p ]$ and $\bbeta ’ = [ \bbeta _ L’ : \bbeta _1’ : \dots : \bbeta _ p’]$. Then the generalized additive model can be represented as $g(\bmu ) = \bX \bbeta $. The roughness penalty matrix is represented as a block diagonal matrix:

\[ \bS _{\blambda } = \begin{bmatrix} \mb{0} & \mb{0} & & \cdots & & \mb{0} \\ \mb{0} & \lambda _1\bS _1 & & \cdots & & \mb{0} \\ & & \ddots & & & \\ \vdots & \vdots & & \lambda _ j\bS _ j & & \vdots \\ & & & & \ddots & \\ \mb{0} & \mb{0} & & \cdots & & \lambda _ p\bS _ p \end{bmatrix} \]

Then the roughness penalty is measured in the quadratic form $\bbeta ’\bS _{\blambda }\bbeta $.

Penalized Likelihood Estimation

Given a fixed vector of smoothing parameters, $\blambda =[\lambda _ i\dots \lambda _ p]’$, you can fit the generalized additive models by the penalized likelihood estimation. In contrast to the maximum likelihood estimation, penalized likelihood estimation obtains an estimate for $\bbeta $ by maximizing the penalized log likelihood,

\[ \ell _ p(\bbeta ) = \ell (\bbeta )-\frac{1}{2}\bbeta ’\bS _{\blambda }\bbeta \]

Any optimization technique that you can use for maximum likelihood estimation can also be used for penalized likelihood estimation. If first-order derivatives are required for the optimization technique, you can compute the gradient as

\[ \frac{\partial \ell _ p}{\partial \bbeta } = \frac{\partial \ell }{\partial \bbeta }-\bS _{\blambda }\bbeta \]

If second-order derivatives are required for the optimization technique, you can compute the Hessian as

\[ \frac{\partial ^2\ell _ p}{\partial \bbeta \partial \bbeta '}= \frac{\partial ^2\ell }{\partial \bbeta \partial \bbeta '}-\bS _{\blambda } \]

In the gradient and Hessian forms, $\partial \ell /\partial \bbeta $ and $\partial ^2\ell /(\partial \bbeta \partial \bbeta ’)$ are the corresponding gradient and Hessian, respectively, for the log-likelihood for generalized linear models. For more information about optimization techniques, see the section Choosing an Optimization Technique.