The GAMPL Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Missing ValuesThin-Plate Regression SplinesGeneralized Additive ModelsModel Evaluation CriteriaFitting AlgorithmsDegrees of FreedomModel InferenceDispersion ParameterTests for Smoothing ComponentsComputational Method: MultithreadingChoosing an Optimization TechniqueDisplayed OutputODS Table NamesODS Graphics
Missing ValuesThin-Plate Regression SplinesGeneralized Additive ModelsModel Evaluation CriteriaFitting AlgorithmsDegrees of FreedomModel InferenceDispersion ParameterTests for Smoothing ComponentsComputational Method: MultithreadingChoosing an Optimization TechniqueDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Technique Descriptions
The following subsections provide details about each optimization technique and follow the same order as Table 7.12.
Trust Region Optimization (TRUREG)
The trust region technique (TRUREG) uses the gradient 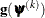 and the Hessian matrix
and the Hessian matrix 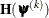 ; thus, it requires that the objective function
; thus, it requires that the objective function 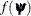 have continuous first- and second-order derivatives inside the feasible region.
have continuous first- and second-order derivatives inside the feasible region.
The trust region technique iteratively optimizes a quadratic approximation to the nonlinear objective function within a hyperelliptic
trust region that has radius 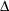 and constrains the step size that corresponds to the quality of the quadratic approximation. The trust region technique that
PROC GAMPL uses is based on Dennis, Gay, and Welsch (1981); Gay (1983); Moré and Sorensen (1983).
and constrains the step size that corresponds to the quality of the quadratic approximation. The trust region technique that
PROC GAMPL uses is based on Dennis, Gay, and Welsch (1981); Gay (1983); Moré and Sorensen (1983).
The trust region technique performs well for small- to medium-sized problems, and it does not need many function, gradient, and Hessian calls. However, if the computation of the Hessian matrix is computationally expensive, either the QUANEW technique or the CONGRA technique might be more efficient.
Newton-Raphson Optimization with Line Search (NEWRAP)
The Newton-Raphson optimization with line search (NEWRAP) technique uses the gradient 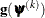 and the Hessian matrix
and the Hessian matrix 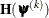 ; thus, it requires that the objective function have continuous first- and second-order derivatives inside the feasible region.
; thus, it requires that the objective function have continuous first- and second-order derivatives inside the feasible region.
If second-order derivatives are computed efficiently and precisely, the NEWRAP technique can perform well for medium-sized to large problems, and it does not need many function, gradient, and Hessian calls.
This technique uses a pure Newton step when the Hessian is positive-definite and when the Newton step reduces the value of the objective function successfully. Otherwise, a combination of ridging and line search is performed to compute successful steps. If the Hessian is not positive-definite, a multiple of the identity matrix is added to the Hessian matrix to make it positive-definite (Eskow and Schnabel 1991).
In each iteration, a line search is performed along the search direction to find an approximate optimum of the objective function. The line-search technique uses quadratic interpolation and cubic extrapolation.
Newton-Raphson Ridge Optimization (NRRIDG)
The Newton-Raphson ridge optimization (NRRIDG) technique uses the gradient 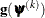 and the Hessian matrix
and the Hessian matrix 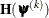 ; thus, it requires that the objective function have continuous first- and second-order derivatives inside the feasible region.
; thus, it requires that the objective function have continuous first- and second-order derivatives inside the feasible region.
This technique uses a pure Newton step when the Hessian is positive-definite and when the Newton step reduces the value of the objective function successfully. If at least one of these two conditions is not satisfied, a multiple of the identity matrix is added to the Hessian matrix.
Because the NRRIDG technique uses an orthogonal decomposition of the approximate Hessian, each iteration of NRRIDG can be slower than an iteration of the NEWRAP technique, which works with a Cholesky decomposition. However, NRRIDG usually requires fewer iterations than NEWRAP.
The NRRIDG technique performs well for small- to medium-sized problems, and it does not require many function, gradient, and Hessian calls. However, if the computation of the Hessian matrix is computationally expensive, either the QUANEW technique or the CONGRA technique might be more efficient.
Dual Quasi-Newton Optimization (QUANEW)
The dual quasi-Newton (QUANEW) technique uses the gradient 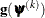 , and it does not need to compute second-order derivatives, because they are approximated. It works well for medium-sized
to moderately large optimization problems, where the objective function and the gradient can be computed much faster than
the Hessian. However, the QUANEW technique requires more iterations in general than the TRUREG, NEWRAP, and NRRIDG techniques,
which compute second-order derivatives. The QUANEW technique provides an appropriate balance between the speed and stability
that are required for most generalized linear model applications.
, and it does not need to compute second-order derivatives, because they are approximated. It works well for medium-sized
to moderately large optimization problems, where the objective function and the gradient can be computed much faster than
the Hessian. However, the QUANEW technique requires more iterations in general than the TRUREG, NEWRAP, and NRRIDG techniques,
which compute second-order derivatives. The QUANEW technique provides an appropriate balance between the speed and stability
that are required for most generalized linear model applications.
The QUANEW technique that PROC GAMPL uses is the dual quasi-Newton technique, which updates the Cholesky factor of an approximate Hessian.
In each iteration, a line search is performed along the search direction to find an approximate optimum. The line-search technique
uses quadratic interpolation and cubic extrapolation to obtain a step size  that satisfies the Goldstein conditions (Fletcher 1987). One of the Goldstein conditions can be violated if the feasible region defines an upper limit of the step size. Violating
the left-side Goldstein condition can affect the positive-definiteness of the quasi-Newton update. In that case, either the
update is skipped or the iterations are restarted by using an identity matrix, resulting in the steepest descent or ascent
search direction.
that satisfies the Goldstein conditions (Fletcher 1987). One of the Goldstein conditions can be violated if the feasible region defines an upper limit of the step size. Violating
the left-side Goldstein condition can affect the positive-definiteness of the quasi-Newton update. In that case, either the
update is skipped or the iterations are restarted by using an identity matrix, resulting in the steepest descent or ascent
search direction.
Double-Dogleg Optimization (DBLDOG)
The double-dogleg optimization (DBLDOG) technique combines the ideas of the quasi-Newton and trust region techniques. In each
iteration, the double-dogleg technique computes the step 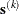 as the linear combination of the steepest descent or ascent search direction
as the linear combination of the steepest descent or ascent search direction 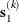 and a quasi-Newton search direction
and a quasi-Newton search direction 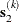 :
:
![\[ \mb{s}^{(k)} = \alpha _1 \mb{s}_1^{(k)} + \alpha _2 \mb{s}_2^{(k)} \]](images/stathpug_hpgam0236.png)
The step must remain within a prespecified trust region radius (Fletcher 1987, p. 107). Thus, the DBLDOG subroutine uses the dual quasi-Newton update but does not perform a line search.
The double-dogleg optimization technique works well for medium-sized to moderately large optimization problems, where the objective function and the gradient can be computed much faster than the Hessian. The implementation is based on Dennis and Mei (1979) and Gay (1983), but it is extended for dealing with boundary and linear constraints. The DBLDOG technique generally requires more iterations than the TRUREG, NEWRAP, and NRRIDG techniques, which require second-order derivatives; however, each of the DBLDOG iterations is computationally cheap. Furthermore, the DBLDOG technique requires only gradient calls for updating of the Cholesky factor of an approximate Hessian.
Conjugate Gradient Optimization (CONGRA)
Second-order derivatives are not required by the CONGRA technique and are not even approximated. The CONGRA technique can
be expensive in function and gradient calls, but it requires only 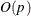 memory for unconstrained optimization. In general, the technique must perform many iterations to obtain a precise solution,
but each of the CONGRA iterations is computationally cheap.
memory for unconstrained optimization. In general, the technique must perform many iterations to obtain a precise solution,
but each of the CONGRA iterations is computationally cheap.
The CONGRA technique should be used for optimization problems that have large p. For the unconstrained or boundary-constrained case, the CONGRA technique requires only 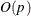 bytes of working memory, whereas all other optimization techniques require order
bytes of working memory, whereas all other optimization techniques require order 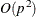 bytes of working memory. During p successive iterations that are uninterrupted by restarts or changes in the working set, the CONGRA technique computes a cycle
of p conjugate search directions. In each iteration, a line search is performed along the search direction to find an approximate
optimum of the objective function. The line-search technique uses quadratic interpolation and cubic extrapolation to obtain
a step size
bytes of working memory. During p successive iterations that are uninterrupted by restarts or changes in the working set, the CONGRA technique computes a cycle
of p conjugate search directions. In each iteration, a line search is performed along the search direction to find an approximate
optimum of the objective function. The line-search technique uses quadratic interpolation and cubic extrapolation to obtain
a step size  that satisfies the Goldstein conditions. One of the Goldstein conditions can be violated if the feasible region defines an
upper limit for the step size.
that satisfies the Goldstein conditions. One of the Goldstein conditions can be violated if the feasible region defines an
upper limit for the step size.
Nelder-Mead Simplex Optimization (NMSIMP)
The Nelder-Mead simplex technique does not use any derivatives and does not assume that the objective function has continuous
derivatives. The objective function itself needs to be continuous. This technique is quite expensive in the number of function
calls, and it might be unable to generate precise results for 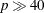 .
.
The original Nelder-Mead simplex technique is implemented and extended to boundary constraints. This technique does not compute the objective for infeasible points, but it changes the shape of the simplex and adapts to the nonlinearities of the objective function. This change contributes to an increased speed of convergence and uses a special termination criterion.