HISTOGRAM Statement: CAPABILITY Procedure
Example 5.11 Computing Capability Indices for Nonnormal Distributions
[See CAPIND in the SAS/QC Sample Library]Standard capability indices such as 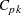 are generally considered meaningful only if the process output has a normal (or reasonably normal) distribution. In practice, however, many processes have nonnormal distributions. This example, which is a continuation of Example 5.9 and Example 5.10, shows how you can use the HISTOGRAM statement to compute generalized capability indices based on fitted nonnormal distributions.
are generally considered meaningful only if the process output has a normal (or reasonably normal) distribution. In practice, however, many processes have nonnormal distributions. This example, which is a continuation of Example 5.9 and Example 5.10, shows how you can use the HISTOGRAM statement to compute generalized capability indices based on fitted nonnormal distributions.
The following statements produce printed output that is partially listed in Output 5.11.1 and Output 5.11.2:
ods graphics off; proc capability data=Plates checkindices(alpha=0.05); specs lsl=0.3 usl= 0.8; histogram Gap / lognormal(indices) noplot; run;
The PROC CAPABILITY statement computes the standard capability indices that are shown in Output 5.11.1.
| Distribution of Plate Gaps |
| Process Capability Indices | |||
|---|---|---|---|
| Index | Value | 95% Confidence Limits | |
| Cp | 0.237112 | 0.190279 | 0.283853 |
| CPL | 0.316422 | 0.203760 | 0.426833 |
| CPU | 0.157803 | 0.059572 | 0.254586 |
| Cpk | 0.157803 | 0.060270 | 0.255336 |
The CHECKINDICES option in the PROC statement requests a goodness-of-fit test for normality in conjunction with the indices and displays the warning that normality is rejected at the significance level 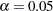 .
.
Example 5.9 concluded that the fitted lognormal distribution summarized in Output 5.9.2 is a good model, so one might consider computing generalized capability indices based on this distribution. These indices are requested with the INDICES option and are shown in Output 5.11.2. Formulas and recommendations for these indices are given in Indices Using Fitted Curves.
| Capability Indices Based on Lognormal Distribution |
|
|---|---|
| Cp | 0.210804 |
| CPL | 0.595156 |
| CPU | 0.124927 |
| Cpk | 0.124927 |
