HISTOGRAM Statement: CAPABILITY Procedure
Adding a Normal Curve to the Histogram
[See CAPHST1 in the SAS/QC Sample Library]This example is a continuation of the preceding example.
The following statements fit a normal distribution from the thickness measurements and superimpose the fitted density curve on the histogram:
ods graphics on; proc capability data=Trans; spec lsl = 3.45 usl = 3.55; histogram / normal; run;
The ODS GRAPHICS ON statement specified before the PROC CAPABILITY statement enables ODS Graphics, so the histogram is created using ODS Graphics instead of traditional graphics.
The NORMAL option summarizes the fitted distribution in the printed output shown in Figure 5.9, and it specifies that the normal curve be displayed on the histogram shown in Figure 5.10.
| Process Capability Analysis of Plating Thickness |
| Parameters for Normal Distribution | ||
|---|---|---|
| Parameter | Symbol | Estimate |
| Mean | Mu | 3.49533 |
| Std Dev | Sigma | 0.032117 |
| Goodness-of-Fit Tests for Normal Distribution | |||||
|---|---|---|---|---|---|
| Test | Statistic | DF | p Value | ||
| Kolmogorov-Smirnov | D | 0.05563823 | Pr > D | >0.150 | |
| Cramer-von Mises | W-Sq | 0.04307548 | Pr > W-Sq | >0.250 | |
| Anderson-Darling | A-Sq | 0.27840748 | Pr > A-Sq | >0.250 | |
| Chi-Square | Chi-Sq | 6.96953022 | 5 | Pr > Chi-Sq | 0.223 |
| Percent Outside Specifications for Normal Distribution | |||
|---|---|---|---|
| Lower Limit | Upper Limit | ||
| LSL | 3.450000 | USL | 3.550000 |
| Obs Pct < LSL | 8.000000 | Obs Pct > USL | 5.000000 |
| Est Pct < LSL | 7.906248 | Est Pct > USL | 4.435722 |
| Quantiles for Normal Distribution | ||
|---|---|---|
| Percent | Quantile | |
| Observed | Estimated | |
| 1.0 | 3.42950 | 3.42061 |
| 5.0 | 3.44300 | 3.44250 |
| 10.0 | 3.45750 | 3.45417 |
| 25.0 | 3.46950 | 3.47367 |
| 50.0 | 3.49600 | 3.49533 |
| 75.0 | 3.51650 | 3.51699 |
| 90.0 | 3.53550 | 3.53649 |
| 95.0 | 3.55300 | 3.54816 |
| 99.0 | 3.57200 | 3.57005 |
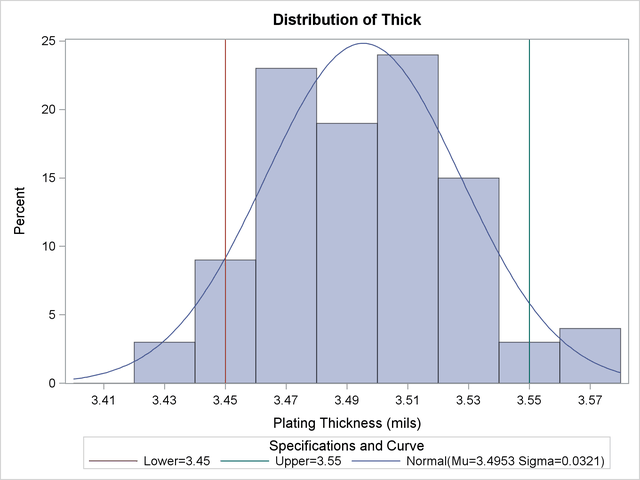
The printed output includes the following:
parameters for the normal curve. The normal parameters
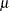and 
are estimated by the sample mean (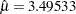
) and the sample standard deviation (
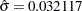). goodness-of-fit tests based on the empirical distribution function (EDF): the Anderson-Darling, Cramer-von Mises, and Kolmogorov-Smirnov tests. The
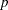-values for these tests are greater than the usual cutoff values of 0.05 and 0.10, indicating that the thicknesses are normally distributed. a chi-square goodness-of-fit test. The
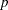-value of 0.223 for this test indicates that the thicknesses are normally distributed. In general EDF tests (when available) are preferable to chi-square tests. See the section EDF Goodness-of-Fit Tests for details. observed and estimated percentages outside the specification limits
observed and estimated quantiles
For details, including formulas for the goodness-of-fit tests, see Printed Output. Note that the NOPRINT option in the PROC CAPABILITY statement suppresses only the printed output with summary statistics for the variable Thick. To suppress the printed output in Figure 5.9, specify the NOPRINT option enclosed in parentheses after the NORMAL option as in Customizing a Histogram.
The NORMAL option is one of many options that you can specify in the HISTOGRAM statement. See the section Syntax: HISTOGRAM Statement for a complete list of options or the section Dictionary of Options for detailed descriptions of options.