Declaration Statements :: SAS/OR(R) 14.1 User's Guide: Mathematical Programming

CONSTRAINT Declaration

CONSTRAINT constraint $\ms {[}$ , …constraint $\ms {]}$ ;

CON constraint $\ms {[}$ , …constraint $\ms {]}$ ;

The constraint declaration defines one or more constraints on expressions in terms of the optimization variables. You can specify multiple constraint declaration statements.

Constraints can have an upper bound, a lower bound, or both bounds. The allowed forms are as follows:

$\ms {[}$ name $\ms {[}$ { index-set } $\ms {]}$ : $\ms {]}$ expression = expression: declares an equality constraint or, when an index-set is specified, a family of equality constraints. The solver attempts to assign values to the optimization variables to make the two expressions equal.
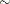$\ms {[}$ name $\ms {[}$ { index-set } $\ms {]}$ : $\ms {]}$ expression $\sim$ = expression: declares a disequality constraint or, when an index-set is specified, a family of disequality constraints. The solver attempts to assign values to the optimization variables to make the two expressions unequal. The CLP solver must be used with this type of constraint.
$\ms {[}$ name $\ms {[}$ { index-set } $\ms {]}$ : $\ms {]}$ expression relation expression: declares an inequality constraint that has a single upper or lower bound. index-set declares a family of inequality constraints. relation is the <=, <, >=, or > operator. When relation is the <= operator, the solver tries to assign optimization variable values so that the value of the left expression is less than or equal to the value of the right expression. When relation is the < operator, the solver tries to assign optimization variable values so that the value of the left expression is less than the value of the right expression. When relation is the >= operator, the solver tries to assign optimization variable values so that the value of the left expression is greater than or equal to the value of the right expression. When relation is the > operator, the solver tries to assign optimization variable values so that the value of the left expression is greater than the value of the right expression. The CLP solver must be used when the < or > operator is specified.
$\ms {[}$ name $\ms {[}$ { index-set } $\ms {]}$ : $\ms {]}$ bound relation body relation bound: declares an inequality constraint that is bounded on both sides, called a range constraint. index-set declares a family of range constraints. relation is the <=, <, >=, or > operator. Both relation operators must match in direction. If the <= or < operator is used in the first position, then a <= or < operator must be used in the second position. If the >= or > operator is used in the first position, then a >= or > operator must be used in the second position. The first bound expression defines the lower bound (if the <= or < operator is used) or the upper bound (if the >= or > operator is used). The second bound defines the upper bound (if the <= or < operator is used) or the lower bound (if the >= or > operator is used). The solver tries to assign optimization variables so that the value of the body expression is in the range between the upper and lower bounds. The CLP solver must be used when the < or > operator is specified.
$\ms {[}$ name $\ms {[}$ { index-set } $\ms {]}$ : $\ms {]}$ predicate: declares a predicate constraint for the CLP solver. See the section Predicates in Chapter 6: The Constraint Programming Solver, for a description of the syntax and meaning of predicates.

Note: You can use the alternate forms from Table 5.10 for the relational operators.

name defines the name for the constraint. Use the name to reference constraint attributes, such as the bounds, elsewhere in the PROC OPTMODEL model. If no name is provided, then a default name is created of the form _ACON_[n], where n is an integer. See the section Constraints for more information.

Here is a simple example that defines a constraint with a lower bound:

proc optmodel;
   var x, y;
   number low;
   con a: x+y >= low;

The following example adds an upper bound:

var x, y;
number low;
con a: low <= x+y <= low+10;

Indexed families of constraints can be defined by specifying an index-set after the name. Any dummy parameters that are declared in the index-set can be referenced in the expressions that define the constraint. A particular member of an indexed family can be specified by using an identifier-expression with a bracketed index list, in the same fashion as array parameters and variables. For example, the following statements create an indexed family of constraints named incr:

proc optmodel;
   number n;
   var x{1..n}
   /* require nondecreasing x values */
   con incr{i in 1..n-1}: x[i+1] >= x[i];

The CON statement in the example creates constraints incr[1] through incr[n–1].

Constraint expressions cannot be defined using functions that return different values each time they are called. See the section Indexing for details.

IMPVAR Declaration

IMPVAR impvar-decl $\ms {[}$ , …impvar-decl $\ms {]}$ ;

The IMPVAR declaration specifies one or more names that refer to optimization expressions in the model. The declared name is called an implicit variable. An implicit variable is useful for structuring models so that complex expressions do not need to be repeated each time they are used. The value of an implicit variable needs to be computed only once instead of at each place where the original expression is used, which helps reduce computational overhead. Implicit variables are evaluated without intervention from the solver.

Multiple IMPVAR declarations are allowed. The names of implicit variables must be distinct from other model declarations, such as variables and constraints. Implicit variables can be used in model expressions in the same places where ordinary variables are allowed.

This is the syntax for an impvar-decl:

name $\ms {[}$ { index-set } $\ms {]}$ = expression

Each impvar-decl declares a name for an implicit variable. The name can be followed by an index-set specification to declare a family of implicit variables. The expression that the name refers to follows. Dummy parameters that are declared in the index-set specification can be used in the expression. The expression can refer to other model components, including variables, the current implicit variable, and other implicit variables.

As an example, in the following model statements the implicit variable total_weight is used in multiple constraints to set a limit on various product quantities, represented by locations in array x:

impvar total_weight = sum{p in PRODUCTS} Weight[p]*x[p];

con prod1_limit: Weight['Prod1'] * x['Prod1'] <= 0.3 * total_weight;
con prod2_limit: Weight['Prod2'] * x['Prod2'] <= 0.25 * total_weight;

MAX and MIN Objective Declarations

MAX name $\ms {[}$ { index-set } $\ms {]}$ = expression;

MIN name $\ms {[}$ { index-set } $\ms {]}$ = expression;

The MAX or MIN declaration specifies an objective for the solver. The name names the objective function for later reference. When a non-array objective declaration is read, the declaration becomes the new objective of the current problem, replacing any previous objective. The solver maximizes an objective that is specified with the MAX keyword and minimizes an objective that is specified with the MIN keyword. An objective is not allowed to have the same name as a parameter or variable. Multiple objectives are permitted, but the solver processes only one objective at a time.

expression specifies the numeric function to maximize or minimize in terms of the optimization-variables. Specify an index-set to declare a family of objectives. Dummy parameters declared in the index-set specification can be used in the following expression.

Objectives can also be used as implicit variables . When used in an expression, an objective name refers to the current value of the named objective function. The value of an unsuffixed objective name can depend on the value of optimization variables, so objective names cannot be used in constant expressions such as variable bounds. You can reference objective names in objective or constraint expressions. For example, the following statements declare two objective names, q and l, which are immediately referred to in the objective declaration of z and the declarations of the constraints.

proc optmodel;
   var x, y;
   min q=(x+y)**2;
   max l=x+2*y;
   min z=q+l;
   con c1: q<=4;
   con c2: l>=2;

Objectives cannot be defined using functions that return different values each time they are called. See the section Indexing for details.

NUMBER, STRING, and SET Parameter Declarations

NUMBER parameter-decl $\ms {[}$ , …parameter-decl $\ms {]}$ ;

STRING parameter-decl $\ms {[}$ , …parameter-decl $\ms {]}$ ;

SET $\ms {[}$ < scalar-type, …scalar-type > $\ms {]}$ parameter-decl $\ms {[}$ , …parameter-decl $\ms {]}$ ;

Parameters provide names for constants. Parameters are declared by specifying the parameter type followed by a list of parameter names. Declarations of parameters that have NUMBER or STRING types start with a scalar-type specification:

NUMBER | NUM ;

STRING | STR ;

The NUM and STR keywords are abbreviations for the NUMBER and STRING keywords, respectively.

The declaration of a parameter that has the set type begins with a set-type specification:

SET $\ms {[}$ < scalar-type, …scalar-type > $\ms {]}$ ;

In a set-type declaration, the SET keyword is followed by a list of scalar-type items that specify the member type. A set with scalar members is specified with a single scalar-type item. A set with tuple members has a scalar-type item for each tuple element. The scalar-type items specify the types of the elements at each tuple position.

If the SET keyword is not followed by a list of scalar-type items, then the set type is determined from the type of the initialization expression. The declared type defaults to SET<NUMBER> if no initialization expression is given or if the expression type cannot be determined.

For any parameter type, the type declaration is followed by a list of parameter-decl items that specify the names of the parameters to declare. In a parameter-decl item the parameter name can be followed by an optional index specification and any necessary options, as follows:

name $\ms {[}$ { index-set } $\ms {]}$ $\ms {[}$ parameter-options $\ms {]}$

The parameter name and index-set can be followed by a list of parameter-options. Dummy parameters declared in the index-set can be used in the parameter-options. The parameter options can be specified with the following forms:

= expression

provides an explicit value for each parameter location. In this case the parameter acts like an alias for the expression value.

INIT expression

specifies a default value that is used when a parameter value is required but no other value has been supplied. For example:

number n init 1;
set s init {'a', 'b', 'c'};

PROC OPTMODEL evaluates the expression for each parameter location the first time the parameter needs to be resolved. The expression is not used when the parameter already has a value.

= [ initializers ]

provides a compact means to define the values for an array, in which each array location value can be individually specified by the initializers.

INIT [ initializers ]

provides a compact means to define multiple default values for an array. Each array location value can be individually specified by the initializers. With this option the array values can still be updated outside the declaration.

The =expression parameter option defines a parameter value by using a formula. The formula can refer to other parameters. The parameter value is updated when the referenced parameters change. The following example shows the effects of the update:

proc optmodel;
   number n;
   set<number> s = 1..n;
   number a{s};
   n = 3;
   a[1] = 2;    /* OK */
   a[7] = 19;   /* error, 7 is not in s */
   n = 10;
   a[7] = 19;   /* OK now */

In the preceding example the value of set s is resolved for each use of array a that has an index. For the first use of a[7], the value 7 is not a member of the set s. However, the value 7 is a member of s at the second use of a[7].

The INIT expression parameter option specifies a default value for a parameter. The following example shows the usage of this option:

proc optmodel;
   num a{i in 1..2} init i**2;
   a[1] = 2;
   put a[*]=;

When the value of a parameter is needed but no other value has been supplied, the default value specified by INIT expression is used, as shown in Figure 5.5.

Figure 5.5: INIT Option: Output

a[1]=2 a[2]=4

Note: Parameter values can also be read from files or specified with assignment statements. However, the value of a parameter that is assigned with the =expression or =[initializers] forms can be changed only by modifying the parameters used in the defining expressions. Parameter values specified by the INIT option can be reassigned freely.

Initializing Arrays

Arrays can be initialized with the =[initializers] or INIT [initializers] forms. These forms are convenient when array location values need to be individually specified. The forms behave the same way, except that the INIT [initializers] form allows the array values to be modified after the declaration. These forms of initialization are used in the following statements:

proc optmodel;
   number a{1..3} = [5 4 7];
   number b{1..3} INIT [5 4 7];
   put a[*]=;
   b[1] = 1;
   put b[*]=;

Each array location receives a different value, as shown in Figure 5.6. The displayed values for b are a combination of the default values from the declaration and the assigned value in the statements.

Figure 5.6: Array Initialization

a[1]=5 a[2]=4 a[3]=7                                                            
b[1]=1 b[2]=4 b[3]=7

Each initializer takes the following form:

$\ms {[}$ [ index ] $\ms {]}$ value

The value specifies the value of an array location and can be a numeric or string constant, a set literal , or an expression enclosed in parentheses.

In array initializers, string constants can be specified using quoted strings. When the string text follows the rules for a SAS name, the text can also be specified without quotation marks. String constants that begin with a digit, contain blanks, or contain other special characters must be specified with a quoted string.

As an example, the following statements define an array parameter that could be used to map numeric days of the week to text strings:

proc optmodel;
   string dn{1..5} =
          [Monday Tuesday Wednesday Thursday Friday];

The optional index in square brackets specifies the index of the array location to initialize. The index specifies one or more numeric or string subscripts. The subscripts allow the same syntactic forms as the value items. Commas can be used to separate index subscripts. For example, location a[1,’abc’] of an array a could be specified with the index [1 abc]. The following example initializes just the diagonal locations in a square array:

proc optmodel;
   number m{1..3,1..3} = [[1 1] 0.1 [2 2] 0.2 [3 3] 0.3];

An index does not need to specify all the subscripts of an array location. If the index begins with a comma, then only the rightmost subscripts of the index need to be specified. The preceding subscripts are supplied from the index that was used by the preceding initializer. This can simplify the initialization of arrays that are indexed by multiple subscripts. For example, you can add new entries to the matrix of the previous example by using the following statements:

proc optmodel;
   number m{1..3,1..3} = [[1 1] 0.1            [,3] 1
                                    [2 2] 0.2  [,3] 2
                                              [3 3] 0.3];

The spacing shows the layout of the example array. The previous example was updated by initializing two more values at m[1,3] and m[2,3].

If an index is omitted, then the next location in the order of the array’s index set is initialized. If the index set has multiple index-set-items, then the rightmost indices are updated before indices to the left are updated. At the beginning of the initializer list, the rightmost index is the first member of the index set. The index set must use a range expression to avoid unpredictable results when an index value is omitted.

The initializers can be followed by commas. The use of commas has no effect on the initialization. The comma can be used to clarify layout. For example, the comma could separate rows in a matrix.

Not every array location needs to be initialized. The locations without an explicit initializer are set to zero for numeric arrays, set to an empty string for string arrays, and set to an empty set for set arrays.

Note: An array location must not be initialized more than once during the processing of the initializer list.

PROBLEM Declaration

PROBLEM name $\ms {[}$ { index-set } $\ms {]}$ $\ms {[}$ FROM problem-id $\ms {]}$ $\ms {[}$ INCLUDE problem-items $\ms {]}$ ;

Problems are declared with the PROBLEM declaration. Problem declarations track an objective, a set of included variables and constraints, and some status information that is associated with the variables and constraints. The problem name can optionally be followed by an index-set to create a family of problems. When a problem is first used (via the USE PROBLEM statement), the specifications from the optional FROM and INCLUDE clauses create the initial set of included variables, constraints, and the problem objective. An empty problem is created if neither clause is specified. The clauses are applied only when the problem is first used with the USE PROBLEM statement.

The FROM clause specifies an existing problem from which to copy the set of included symbols. The problem-id is an identifier expression . The dropped and fixed status for these symbols in the specified problem is also copied.

The INCLUDE clause specifies a list of variables, constraints, and objectives to include in the problem. These items are included with default status (unfixed and undropped) which overrides the status from the FROM clause, if it exists. Each item is specified with one of the following forms:

identifier-expression: includes the specified items in the problem. The identifier-expression can be a symbol name or an array symbol with explicit index. If an array symbol is used without an index, then all array elements are included.
{ index-set } identifier-expression: includes the specified subset of items in the problem. The item specified by the identifier-expression is added to the problem for each member of the index-set . The dummy parameters from the index-set can be used in the indexing of the identifier-expression. If the identifier-expression is an array symbol without indexing, then the index-set provides the indices for the included locations.

You can use the FROM and INCLUDE clauses to designate the initial objective for a problem. The objective is copied from the problem designated by the FROM clause, if present. Then the INCLUDE clause, if any, is applied, and the last objective specified becomes the initial objective.

The following statements declare some problems with a variable x and different objectives to illustrate some of the ways of including model components. Note that the statements use the predeclared problem _START_ to avoid resetting the objective in prob2 when the objective z3 is declared.

proc optmodel;
   problem prob1;
   use problem prob1;
   var x >= 0;             /* included in prob1 */
   min z1 = (x-1)**2;      /* included in prob1 */
   expand;                 /* prob1 contains x, z1 */

   problem prob2 from prob1;
   use problem prob2;      /* includes x, z1 */
   min z2 = (x-2)**2;      /* resets prob2 objective to z2 */
   expand;                 /* prob2 contains x, z2 */

   use problem _start_;    /* don't modify prob2 */
   min z3 = (x-3)**2;
   problem prob3 include x z3;
   use problem prob3;
   expand;                 /* prob3 contains x, z3 */

See the section Multiple Subproblems for more details about problem processing.

VAR Declaration

VAR var-decl $\ms {[}$ , …var-decl $\ms {]}$ ;

The VAR statement declares one or more optimization variables. Multiple VAR statements are permitted. A variable is not allowed to have the same name as a parameter or constraint.

Each var-decl specifies a variable name. The name can be followed by an array index-set specification and then variable options. Dummy parameters declared in the index set specification can be used in the following variable options.

Here is the syntax for a var-decl:

name $\ms {[}$ { index-set } $\ms {]}$ $\ms {[}$ var-options $\ms {]}$

For example, the following statements declare a group of 100 variables, x[1]–x[100]:

proc optmodel;
   var x{1..100};

Here are the available variable options:

INIT expression: sets an initial value for the variable. The expression is used only the first time the value is required. If no initial value is specified, then 0 is used by default.
>= expression: sets a lower bound for the variable value. The default lower bound is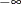 $-\infty$ , or 0 if the BINARY option is used.
<= expression: sets an upper bound for the variable value. The default upper bound is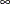 $\infty$ , or 1 if the BINARY option is used.
INTEGER: requests that the solver assign the variable an integer value.
BINARY: requests that the solver assign the variable an integer value within default bounds of 0 to 1.

For example, the following statements declare a variable that has an initial value of 0.5. The variable is bounded by 0 and 1:

proc optmodel;
   var x init 0.5 >= 0 <= 1;

The values of the bounds can be determined later by using suffixed references to the variable. For example, the upper bound for variable x can be referred to as x.ub. In addition, the bounds options can be overridden by explicit assignment to the suffixed variable name. Suffixes are described further in the section Suffixes. Note that the bounds for integer and binary variables are rounded to integers according to the value that you specify in the PROC OPTMODEL option INTFUZZ= .

When used in an expression, an unsuffixed variable name refers to the current value of the variable. Unsuffixed variables are not allowed in the expressions for options that define variable bounds or initial values. Such expressions have values that must be fixed during execution of the solver.

The OPTMODEL Procedure