The OPTMODEL Procedure

This example illustrates how to convert PROC NLP code that handles arrays into PROC OPTMODEL form. The following PROC NLP model finds an equilibrium state for a mixture of chemicals. The same model is used in "Example 7.8: Chemical Equilibrium" in Chapter 6: The NLP Procedure in SAS/OR 14.1 User's Guide: Mathematical Programming Legacy Procedures.

proc nlp tech=tr pall;
   array c[10] -6.089 -17.164 -34.054  -5.914 -24.721
              -14.986 -24.100 -10.708 -26.662 -22.179;
   array x[10] x1-x10;
   min y;
   parms x1-x10 = .1;
   bounds 1.e-6 <= x1-x10;
   lincon 2. = x1 + 2. * x2 + 2. * x3 + x6 + x10,
          1. = x4 + 2. * x5 + x6 + x7,
          1. = x3 + x7  + x8 + 2. * x9 + x10;
   s = x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10;
   y = 0.;
   do j = 1 to 10;
      y = y + x[j] * (c[j] + log(x[j] / s));
   end;
run;

The following statements show a corresponding PROC OPTMODEL model:

proc optmodel;
   set CMP = 1..10;
   number c{CMP} = [-6.089 -17.164 -34.054  -5.914 -24.721
                    -14.986 -24.100 -10.708 -26.662 -22.179];
   var x{CMP} init 0.1 >= 1.e-6;
   con 2. = x[1] + 2. * x[2] + 2. * x[3] + x[6] + x[10],
       1. = x[4] + 2. * x[5] + x[6] + x[7],
       1. = x[3] + x[7]  + x[8] + 2. * x[9] + x[10];
   /* replace the variable s in the PROC NLP model */
   impvar s = sum{i in CMP} x[i];
   min y = sum{j in CMP} x[j] * (c[j] + log(x[j] / s));
   solve;
   print x y;

The PROC OPTMODEL model uses the set CMP to represent the set of compounds, which are numbered 1 to 10 in the example. The array c was initialized by using the equivalent PROC OPTMODEL syntax. The individual array locations could also have been initialized by assignment or by READ DATA statements.

The VAR declaration for variable x combines the VAR and BOUNDS statements of the PROC NLP model. The index set of the array is based on the set of compounds CMP to simplify changes to the model.

The linear constraints are similar in form to the PROC NLP model. However, the PROC OPTMODEL version uses the array form of the variable names because it treats arrays as distinct variables, not as aliases of lists of scalar variables.

The implicit variable s replaces the intermediate variable of the same name in the PROC NLP model. This is an example of translating an intermediate variable from the other models to PROC OPTMODEL. An alternative way is to use an additional constraint for every intermediate variable. Instead of declaring objective s as in the preceding statements, you can use the following statements:

   . . .
   var s;
   con s = sum{i in CMP} x[i];
   . . .

Note that this alternative formulation passes an extra variable and constraint to the solver. This formulation can sometimes be solved more efficiently, depending on the characteristics of the model.

The PROC OPTMODEL version uses a SUM operator over the set CMP, which enhances the flexibility of the model to accommodate possible changes in the set of compounds.

In the PROC NLP model, the objective function y is determined by an explicit loop. The DO loop in PROC NLP is replaced by a SUM aggregation operation in PROC OPTMODEL. The accumulation in the PROC NLP model is now performed by PROC OPTMODEL by using the SUM operator.

This PROC OPTMODEL model can be generalized further. Note that the array initialization and constraints assume a fixed set of compounds. You can rewrite the model to handle an arbitrary number of compounds and chemical elements. The new model loads the linear constraint coefficients from a data set along with the objective coefficients for the parameter c, as follows:

data comp;
   input c a_1 a_2 a_3;
   datalines;
-6.089   1 0 0
-17.164  2 0 0
-34.054  2 0 1
-5.914   0 1 0
-24.721  0 2 0
-14.986  1 1 0
-24.100  0 1 1
-10.708  0 0 1
-26.662  0 0 2
-22.179  1 0 1
;

data atom;
   input b @@;
   datalines;
2. 1. 1.
;

proc optmodel;
   set CMP;
   set ELT;
   number c{CMP};
   number a{ELT,CMP};
   number b{ELT};
   read data atom into ELT=[_n_] b;
   read data comp into CMP=[_n_]
        c {i in ELT} < a[i,_n_]=col("a_"||i) >;
   var x{CMP} init 0.1 >= 1.e-6;
   con bal{i in ELT}: b[i] = sum{j in CMP} a[i,j]*x[j];
   impvar s = sum{i in CMP} x[i];
   min y = sum{j in CMP} x[j] * (c[j] + log(x[j] / s));
   print a b;
   solve;
   print x;

This version adds coefficients for the linear constraints to the COMP data set. The data set variable a_n represents the number of atoms in the compound for element n. The READ DATA statement for COMP uses the iterated column syntax to read each of the data set variables a_n into the appropriate location in the array a. In this example the expanded data set variable names are a_1, a_2, and a_3.

The preceding version also adds a new set, ELT, of chemical elements and a numeric parameter, b, that represents the left-hand side of the linear constraints. The data values for the parameters ELT and b are read from the data set ATOM. The model can handle varying sets of chemical elements because of this extra data set and the new parameters.

The linear constraints have been converted to a single, indexed family of constraints. One constraint is applied for each chemical element in the set ELT. The constraint expression uses a simple form that applies generally to linear constraints. The following PRINT statement in the model shows the values that are read from the data sets to define the linear constraints:

   print a b;

The PRINT statements in the model produce the results shown in Output 5.8.1.

In the preceding model, the chemical elements and compounds are designated by numbers. So in the PRINT output, for example, the row that is labeled "3" represents the amount of the compound 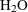. PROC OPTMODEL is capable of using more symbolic strings to designate array indices. The following version of the model uses strings to index arrays:

data comp;
   input name $ c a_h a_n a_o;
   datalines;
H     -6.089   1 0 0
H2    -17.164  2 0 0
H2O   -34.054  2 0 1
N     -5.914   0 1 0
N2    -24.721  0 2 0
NH    -14.986  1 1 0
NO    -24.100  0 1 1
O     -10.708  0 0 1
O2    -26.662  0 0 2
OH    -22.179  1 0 1
;
data atom;
   input name $ b;
   datalines;
H  2.
N  1.
O  1.
;
proc optmodel;
  set<string> CMP;
  set<string> ELT;
  number c{CMP};
  number a{ELT,CMP};
  number b{ELT};
  read data atom into ELT=[name] b;
  read data comp into CMP=[name]
       c {i in ELT} < a[i,name]=col("a_"||i) >;
  var x{CMP} init 0.1 >= 1.e-6;
  con bal{i in ELT}: b[i] = sum{j in CMP} a[i,j]*x[j];
  impvar s = sum{i in CMP} x[i];
  min y = sum{j in CMP} x[j] * (c[j] + log(x[j] / s));
  solve;
  print x;

In this model, the sets CMP and ELT are now sets of strings. The data sets provide the names of the compounds and elements. The names of the data set variables for atom counts in the data set COMP now include the chemical element symbol as part of their spelling. For example, the atom count for element H (hydrogen) is named a_h. Note that these changes did not require any modification to the specifications of the linear constraints or of the objective.

The PRINT statement in the preceding statements produces the results shown in Output 5.8.2. The indices of variable x are now strings that represent the actual compounds.