The OPTMODEL Procedure

A Transportation Problem

You can easily translate the symbolic formulation of a problem into the OPTMODEL procedure. Consider the transportation problem, which is mathematically modeled as the following linear programming problem:

$\begin{array}{lrcllc} \displaystyle \mathop {\textrm{minimize}}& {\displaystyle \mathop \sum _{i\in O, j \in D}}c_{ij}x_{ij}& & & & \\ \textrm{subject to}& {\displaystyle \mathop \sum _{j \in D}x_{ij}} & = & a_ i, & \quad \forall i \in O & (\mr{SUPPLY}) \\ & {\displaystyle \mathop \sum _{i \in O}x_{ij}} & = & b_ j, & \quad \forall j \in D & (\mr{DEMAND}) \\ & x_{ij} & \geq & 0, & \quad \forall (i,j) \in O \times D & \end{array}$

where O is the set of origins, D is the set of destinations, 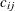$c_{ij}$ is the cost to transport one unit from i to j, 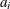$a_ i$ is the supply of origin i, 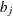$b_ j$ is the demand of destination j, and 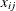$x_{ij}$ is the decision variable for the amount of shipment from i to j.

Here is a very simple example. The cities in the set O of origins are Detroit and Pittsburgh. The cities in the set D of destinations are Boston and New York. The cost matrix, supply, and demand are shown in Table 5.2.

Table 5.2: A Transportation Problem

	Boston	New York	Supply
Detroit	30	20	200
Pittsburgh	40	10	100
Demand	150	150

The problem is compactly and clearly formulated and solved by using the OPTMODEL procedure with the following statements:

proc optmodel;
   /* specify parameters */
   set O={'Detroit','Pittsburgh'};
   set D={'Boston','New York'};
   number c{O,D}=[30 20
                  40 10];
   number a{O}=[200 100];
   number b{D}=[150 150];
   /* model description */
   var x{O,D} >= 0;
   min total_cost = sum{i in O, j in D}c[i,j]*x[i,j];
   constraint supply{i in O}: sum{j in D}x[i,j]=a[i];
   constraint demand{j in D}: sum{i in O}x[i,j]=b[j];
   /* solve and output */
   solve;
   print x;

The output is shown in Figure 5.4.

Figure 5.4: Solution to the Transportation Problem

The OPTMODEL Procedure

Problem Summary
Objective Sense	Minimization
Objective Function	total_cost
Objective Type	Linear

Number of Variables	4
Bounded Above	0
Bounded Below	4
Bounded Below and Above	0
Free	0
Fixed	0

Number of Constraints	4
Linear LE (<=)	0
Linear EQ (=)	4
Linear GE (>=)	0
Linear Range	0

Constraint Coefficients	8

Performance Information
Execution Mode	Single-Machine
Number of Threads	1

Solution Summary
Solver	LP
Algorithm	Dual Simplex
Objective Function	total_cost
Solution Status	Optimal
Objective Value	6500

Primal Infeasibility	0
Dual Infeasibility	0
Bound Infeasibility	0

Iterations	0
Presolve Time	0.00
Solution Time	0.00

x
	Boston	New York
Detroit	150	50
Pittsburgh	0	100