The OPTMODEL Procedure
- Overview
-
Getting Started
-
Syntax
-
DetailsNamed ParametersIndexingTypesNamesParametersExpressionsIdentifier ExpressionsFunction ExpressionsIndex SetsOPTMODEL Expression ExtensionsConditions of OptimalityData Set Input/OutputControl FlowFormatted OutputODS Table and Variable NamesConstraintsSuffixesInteger Variable SuffixesDual ValuesReduced CostsPresolverModel UpdateMultiple SubproblemsMultiple SolutionsProblem SymbolsOPTMODEL OptionsAutomatic DifferentiationConversionsFCMP RoutinesMore on Index SetsThreaded and Distributed ProcessingMacro Variable _OROPTMODEL_Rewriting PROC NLP Models for PROC OPTMODEL
-
Examples
- References
The Rosenbrock Problem
You can use parameters to produce a clear formulation of a problem. Consider the Rosenbrock problem,
![\[ \displaystyle \mathop {\textrm{minimize}}\; f(x_1, x_2) = \alpha \, (x_2 - x_1^2)^2 + (1 - x_1)^2 \]](images/ormpug_optmodel0016.png)
where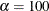 
is a parameter (constant), 
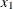and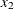 
are optimization variables (whose values are to be determined), and 
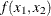is an objective function.
Here is a PROC OPTMODEL program that solves the Rosenbrock problem:
proc optmodel;
number alpha = 100; /* declare parameter */
var x {1..2}; /* declare variables */
/* objective function */
min f = alpha*(x[2] - x[1]**2)**2 +
(1 - x[1])**2;
/* now run the solver */
solve;
print x;
quit;
The PROC OPTMODEL output is shown in Figure 5.3.
Figure 5.3: Rosenbrock Function Results