The PANEL Procedure

Heteroscedasticity- and Autocorrelation-Consistent Covariance Matrices

The HAC option in the MODEL statement selects the type of heteroscedasticity- and autocorrelation-consistent covariance matrix. As with the HCCME option, an estimator of the middle expression 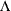$\Lambda $ in sandwich form is needed. With the HAC option, it is estimated as

\[ \Lambda _{\mr{HAC}}=a\sum _{i = 1} ^{N} \sum _{t=1}^{T_ i} \hat{\epsilon }_{it} ^{2}\mb{x} _{it} \mb{x} _{it} ^{'} +a\sum _{i = 1} ^{N} \sum _{t=1}^{T_ i} \sum _{s=1}^{t-1} k(\frac{s-t}{b})\hat{\epsilon }_{it}\hat{\epsilon }_{is}\left(\mb{x} _{it} \mb{x} _{is} ^{'}+\mb{x} _{is} \mb{x} _{it} ^{'}\right) \]

, where $k(.)$ is the real-valued kernel function[6], b is the bandwidth parameter, and a is the adjustment factor of small sample degrees of freedom (that is, $a=1$ if the ADJUSTDF option is not specified and otherwise $a=NT/(NT-k)$, where k is the number of parameters including dummy variables). The types of kernel functions are listed in Table 27.2.

Table 27.2: Kernel Functions

Kernel Name

Equation

Bartlett

$k(x)=\left\{ \begin{array}{ll} 1-|x| & |x|\leq 1 \\ 0 & \text {otherwise} \end{array} \right.$

Parzen

$k(x)=\left\{ \begin{array}{ll} 1-6x^2+6|x|^3 & 0\leq |x| \leq 1/2 \\ 2(1-|x|)^3 & 1/2 \leq |x| \leq 1 \\ 0 & \text {otherwise} \end{array} \right.$

Quadratic spectral

$k(x)=\frac{25}{12\pi ^2x^2} \left( \frac{\sin {(6\pi x/5)}}{6\pi x/5} - \cos {(6\pi x/5)} \right)$

Truncated

$k(x)=\left\{ \begin{array}{ll} 1 & |x|\leq 1 \\ 0 & \text {otherwise} \end{array} \right.$

Tukey-Hanning

$k(x)=\left\{ \begin{array}{ll} \left(1+\cos {(\pi x)}\right)/2 & |x|\leq 1 \\ 0 & \text {otherwise} \end{array} \right.$


When the BANDWIDTH=ANDREWS option is specified, the bandwidth parameter is estimated as shown in Table 27.3.

Table 27.3: Bandwidth Parameter Estimation

Kernel Name

Bandwidth Parameter

Bartlett

$b = 1.1447(\alpha (1)T)^{1/3}$

Parzen

$b = 2.6614(\alpha (2)T)^{1/5}$

Quadratic spectral

$b = 1.3221(\alpha (2)T)^{1/5}$

Truncated

$b = 0.6611(\alpha (2)T)^{1/5}$

Tukey-Hanning

$b = 1.7462(\alpha (2)T)^{1/5}$


Let $\{ g_{ait}\} $ denote each series in $\{ g_{it}=\hat{\epsilon }_{it} \mb{x} _{it}\} $, and let $(\rho _ a,\sigma _ a^2)$ denote the corresponding estimates of the autoregressive and innovation variance parameters of the AR(1) model on $\{ g_{ait}\} $, $a=1,...,k$, where the AR(1) model is parameterized as $g_{ait}=\rho g_{ait-1} + \epsilon _{ait}$ with $Var(\epsilon _{ait})=\sigma _ a^2$. The $\alpha (1)$ and $\alpha (2)$ are estimated with the following formulas:

\[ \alpha (1) = \frac{\sum _{a=1}^ k{\frac{4\rho _ a^{2}\sigma _ a^4}{(1-\rho _ a)^6(1+\rho _ a)^2}}}{\sum _{a=1}^ k{\frac{\sigma _ a^4}{(1-\rho _ a)^4}}} \\ \alpha (2) = \frac{\sum _{a=1}^ k{\frac{4\rho _ a^{2}\sigma _ a^4}{(1-\rho _ a)^8}}}{\sum _{a=1}^ k{\frac{\sigma _ a^4}{(1-\rho _ a)^4}}} \]

When you specify BANDWIDTH=NEWEYWEST94, according to Newey and West (1994) the bandwidth parameter is estimated as shown in Table 27.4.

Table 27.4: Bandwidth Parameter Estimation

Kernel Name

Bandwidth Parameter

Bartlett

$b = 1.1447(\{ s_1/s_0\} ^2T)^{1/3}$

Parzen

$b = 2.6614(\{ s_1/s_0\} ^2T)^{1/5}$

Quadratic spectral

$b = 1.3221(\{ s_1/s_0\} ^2T)^{1/5}$

Truncated

$b = 0.6611(\{ s_1/s_0\} ^2T)^{1/5}$

Tukey-Hanning

$b = 1.7462(\{ s_1/s_0\} ^2T)^{1/5}$


The $s_1$ and $s_0$ are estimated with the following formulas:

\[ s_1 = 2\sum _{j=1}^ n{j\sigma _ j} \\ s_0 = \sigma _0+2\sum _{j=1}^ n{\sigma _ j} \]

where n is the lag selection parameter and is determined by kernels, as listed in Table 27.5.

Table 27.5: Lag Selection Parameter Estimation

Kernel Name

Lag Selection Parameter

Bartlett

$n = c(T/100)^{2/9}$

Parzen

$n = c(T/100)^{4/25}$

Quadratic Spectral

$n = c(T/100)^{2/25}$

Truncated

$n = c(T/100)^{1/5}$

Tukey-Hanning

$n = c(T/100)^{1/5}$


The c in Table 27.5 is specified by the C= option; by default, C=12.

The $\sigma _ j$ is estimated with the equation

\[ \sigma _ j = T^{-1}\sum _{t=j+1}^{T}{\left(\sum _{a=i}^ k{g_{at}}\sum _{a=i}^ k{g_{at-j}}\right)}, j=0, ..., n \]

where $g_{at}$ is the same as in the Andrews method and i is 1 if the NOINT option in the MODEL statement is specified, and 2 otherwise.

When you specify BANDWIDTH=SAMPLESIZE, the bandwidth parameter is estimated with the equation

\[ b = \left\{ \begin{array}{ l l } \left\lfloor {\gamma T^{r} + c} \right\rfloor & \text {if BANDWIDTH=SAMPLESIZE(INT) option is specified} \\ \gamma T^{r} + c & \text {otherwise} \end{array} \right. \]

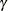where T is the sample size, $\left\lfloor {x} \right\rfloor $ is the largest integer less than or equal to x, and $\gamma $, r, and c are values specified by BANDWIDTH=SAMPLESIZE(GAMMA=, RATE=, CONSTANT=) options, respectively.

If the PREWHITENING option is specified in the MODEL statement, $g_{it} $ is prewhitened by the VAR(1) model,

\[ g_{it} = A_{i} g_{i,t-1} + w_{it} \]

Then $\Lambda _{\mr{HAC}}$ is calculated by

\[ \Lambda _{\mr{HAC}}=a\sum _{i = 1} ^{N}\left\{ \left(\sum _{t=1}^{T_{i}}{w_{it} w_{it}’}+\sum _{t=1}^{T_{i}}{\sum _{s=1}^{t-1}{k(\frac{s-t}{b})\left(w_{it} w_{is}’ + w_{is} w_{it}’\right)}}\right)(I-A_{i})^{-1}((I-A_{i})^{-1})’\right\} \]


[6] The HCCME=0 with CLUSTER option sets $k(.)=1$.