The AUTOREG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesAutoregressive Error ModelAlternative Autocorrelation Correction MethodsGARCH ModelsHeteroscedasticity- and Autocorrelation-Consistent Covariance Matrix EstimatorGoodness-of-Fit Measures and Information CriteriaTestingPredicted ValuesOUT= Data SetOUTEST= Data SetPrinted OutputODS Table NamesODS Graphics
Missing ValuesAutoregressive Error ModelAlternative Autocorrelation Correction MethodsGARCH ModelsHeteroscedasticity- and Autocorrelation-Consistent Covariance Matrix EstimatorGoodness-of-Fit Measures and Information CriteriaTestingPredicted ValuesOUT= Data SetOUTEST= Data SetPrinted OutputODS Table NamesODS Graphics -
Examples

- References
MODEL Statement
MODEL dependent = regressors / options ;
The MODEL statement specifies the dependent variable and independent regressor variables for the regression model. If no independent variables are specified in the MODEL statement, only the mean is fitted. (This is a way to obtain autocorrelations of a series.)
Models can be given labels of up to eight characters. Model labels are used in the printed output to identify the results for different models. The model label is specified as follows:
label : MODEL …;
The following options can be used in the MODEL statement after a slash (/).
Autoregressive Error Options
GARCH Estimation Options
- DIST=value
-
specifies the distribution assumed for the error term in GARCH-type estimation. If no GARCH= option is specified, the option is ignored. If EGARCH is specified, the distribution is always the normal distribution. The values of the DIST= option are as follows:
- T
-
specifies Student’s t distribution.
- NORMAL
-
specifies the standard normal distribution. The default is DIST=NORMAL.
- GARCH=(option-list)
-
specifies a GARCH-type conditional heteroscedasticity model. The GARCH= option in the MODEL statement specifies the family of ARCH models to be estimated. The GARCH
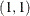 regression model is specified in the following statement:
regression model is specified in the following statement:
model y = x1 x2 / garch=(q=1,p=1);
When you want to estimate the subset of ARCH terms, such as ARCH
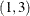 , you can write the SAS statement as follows:
, you can write the SAS statement as follows:
model y = x1 x2 / garch=(q=(1 3));
With the TYPE= option, you can specify various GARCH models. The IGARCH
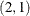 model without trend in variance is estimated as follows:
model without trend in variance is estimated as follows:
model y = / garch=(q=2,p=1,type=integ,noint);
The following options can be used in the GARCH=( ) option. The options are listed within parentheses and separated by commas.
-
Q=number
Q=(number-list) -
specifies the order of the process or the subset of ARCH terms to be fitted.
-
P=number
P=(number-list) -
specifies the order of the process or the subset of GARCH terms to be fitted. If only the P= option is specified, P= option is ignored and Q=1 is assumed.
- TYPE=value
-
specifies the type of GARCH model. The values of the TYPE= option are as follows:
- EXP | EGARCH
-
specifies the exponential GARCH or EGARCH model.
- INTEGRATED | IGARCH
-
specifies the integrated GARCH or IGARCH model.
- NELSON | NELSONCAO
-
specifies the Nelson-Cao inequality constraints.
- NONNEG
-
specifies the GARCH model with nonnegativity constraints.
- POWER | PGARCH
-
specifies the power GARCH or PGARCH model.
- QUADR | QUADRATIC | QGARCH
-
specifies the quadratic GARCH or QGARCH model.
- STATIONARY
-
constrains the sum of GARCH coefficients to be less than 1.
- THRES | THRESHOLD | TGARCH
-
specifies the threshold GARCH or TGARCH model.
The default is TYPE=NELSON.
- MEAN=value
-
specifies the functional form of the GARCH-M model. The values of the MEAN= option are as follows:
- LINEAR
-
specifies the linear function:
![\[ y_{t} = \mb {x} _{t}’{\beta } + {\delta }h_{t} + {\epsilon }_{t} \]](images/etsug_autoreg0051.png)
- LOG
-
specifies the log function:
![\[ y_{t} = \mb {x} _{t}’{\beta } + {\delta }\ln (h_{t}) + {\epsilon }_{t} \]](images/etsug_autoreg0052.png)
- SQRT
-
specifies the square root function:
![\[ y_{t} = \mb {x} _{t}’{\beta } + {\delta }\sqrt {h_{t}} + {\epsilon }_{t} \]](images/etsug_autoreg0053.png)
- NOINT
-
suppresses the intercept parameter in the conditional variance model. This option is valid only with the TYPE=INTEG option.
- STARTUP=MSE | ESTIMATE
-
requests that the positive constant c for the start-up values of the GARCH conditional error variance process be estimated. By default or if STARTUP=MSE is specified, the value of the mean squared error is used as the default constant.
- TR
-
uses the trust region method for GARCH estimation. This algorithm is numerically stable, though computation is expensive. The double quasi-Newton method is the default.
Printing Options
- ALL
-
ARCHTEST
ARCHTEST=(option-list) -
specifies tests for the absence of ARCH effects. The following options can be used in the ARCHTEST=( ) option. The options are listed within parentheses and separated by commas.
- QLM | QLMARCH
-
requests the Q and Engle’s LM tests.
- LK | LKARCH
-
requests Lee and King’s ARCH tests.
- WL | WLARCH
-
requests Wong and Li’s ARCH tests.
- ALL
-
requests all ARCH tests, namely Q and Engle’s LM tests, Lee and King’s tests, and Wong and Li’s tests.
If ARCHTEST is defined without additional suboptions, it requests the Q and Engle’s LM tests. That is,the statement
model return = x1 x2 / archtest;
is equivalent to the statement
model return = x1 x2 / archtest=(qlm);
The following statement requests Lee and King’s tests and Wong and Li’s tests:
model return = / archtest=(lk,wl);
-
BDS
BDS=(option-list) -
specifies Brock-Dechert-Scheinkman (BDS) tests for independence. The following options can be used in the BDS=( ) option. The options are listed within parentheses and separated by commas.
- M=number
-
specifies the maximum number of the embedding dimension. The BDS tests with embedding dimension from
 to M are calculated. M must be an integer between 2 and 20. The default value of the M= suboption is 20.
to M are calculated. M must be an integer between 2 and 20. The default value of the M= suboption is 20.
- D=number
-
specifies the parameter to determine the radius for BDS test. The BDS test sets up the radius as
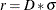 , where
, where  is the standard deviation of the time series to be tested. By default, D=1.5.
is the standard deviation of the time series to be tested. By default, D=1.5.
- PVALUE=DIST | SIM
-
specifies the way to calculate the p-values. By default or if PVALUE=DIST is specified, the p-values are calculated according to the asymptotic distribution of BDS statistics (that is, the standard normal distribution). Otherwise, for samples of size less than 500, the p-values are obtained though Monte Carlo simulation.
- Z=value
-
specifies the type of the time series (residuals) to be tested. You can specify the following values:
- Y
-
specifies the regressand.
- RO
-
specifies the OLS residuals.
- R
-
specifies the residuals of the final model.
- RM
-
specifies the structural residuals of the final model.
- SR
-
specifies the standardized residuals of the final model, defined by residuals over the square root of the conditional variance.
The default is Z=Y.
If BDS is defined without additional suboptions, all suboptions are set as default values. That is, the following two statements are equivalent:
model return = x1 x2 / nlag=1 BDS;
model return = x1 x2 / nlag=1 BDS=(M=20, D=1.5, PVALUE=DIST, Z=Y);
To do the specification check of a GARCH(1,1) model, you can write the SAS statement as follows:
model return = / garch=(p=1,q=1) BDS=(Z=SR);
-
BP
BP=(option-list) -
specifies Bai-Perron (BP) tests for multiple structural changes, introduced in Bai and Perron (1998). You can specify the following options in the BP=( ) option, in parentheses and separated by commas.
- EPS=number
-
specifies the minimum length of regime; that is, if EPS=
 , for any
, for any 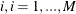 ,
, 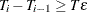 , where
, where 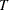 is the sample size;
is the sample size; 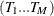 are the break dates; and
are the break dates; and 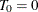 and
and 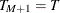 . The default is EPS=0.05.
. The default is EPS=0.05.
- ETA=number
-
specifies that the second method is to be used in the calculation of the
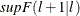 test, and the minimum length of regime for the new additional break date is
test, and the minimum length of regime for the new additional break date is 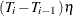 if ETA=
if ETA=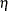 and the new break date is in regime
and the new break date is in regime 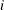 for the given break dates
for the given break dates 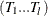 . The default value of the ETA= suboption is the missing value; i.e., the first method is to be used in the calculation of
the
. The default value of the ETA= suboption is the missing value; i.e., the first method is to be used in the calculation of
the 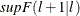 test and, no matter which regime the new break date is in, the minimum length of regime for the new additional break date
is
test and, no matter which regime the new break date is in, the minimum length of regime for the new additional break date
is 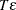 when EPS=
when EPS= .
.
- HAC<(option-list)>
-
specifies that the heteroscedasticity- and autocorrelation-consistent estimator be applied in the estimation of the variance covariance matrix and the confidence intervals of break dates. When the HAC option is specified, you can specify the following options within parentheses and separated by commas:
- KERNEL=value
-
specifies the type of kernel function. You can specify the following values:
- BARTLETT
-
specifies the Bartlett kernel function.
- PARZEN
-
specifies the Parzen kernel function.
- QUADRATICSPECTRAL | QS
-
specifies the quadratic spectral kernel function.
- TRUNCATED
-
specifies the truncated kernel function.
- TUKEYHANNING | TUKEY | TH
-
specifies the Tukey-Hanning kernel function.
The default is KERNEL=QUADRATICSPECTRAL.
- KERNELLB=number
-
specifies the lower bound of the kernel weight value. Any kernel weight less than this lower bound is regarded as zero, which accelerates the calculation for big samples, especially for the quadratic spectral kernel. The default is KERNELLB=0.
- BANDWIDTH=value
-
specifies the fixed bandwidth value or bandwidth selection method to use in the kernel function. You can specify the following values:
- ANDREWS91 | ANDREWS
-
specifies the Andrews (1991) bandwidth selection method.
- NEWEYWEST94 | NW94 <(C=number)>
-
specifies the Newey and West (1994) bandwidth selection method. You can specify the C= option in parentheses to calculate the lag selection parameter; the default is C=12.
- SAMPLESIZE | SS <(option-list)>
-
specifies that the bandwidth be calculated according to the following equation, based on the sample size:
![\[ b=\gamma T^{r} + c \]](images/etsug_autoreg0070.png)
where
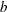 is the bandwidth parameter and
is the bandwidth parameter and 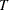 is the sample size, and
is the sample size, and 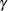 ,
,  , and
, and  are values specified by the following options within parentheses and separated by commas.
are values specified by the following options within parentheses and separated by commas.
- GAMMA=number
-
specifies the coefficient
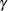 in the equation. The default is
in the equation. The default is 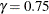 .
.
- RATE=number
-
specifies the growth rate
 in the equation. The default is
in the equation. The default is 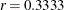 .
.
- CONSTANT=number
-
specifies the constant
 in the equation. The default is
in the equation. The default is 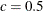 .
.
- INT
-
specifies that the bandwidth parameter must be integer; that is,
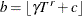 , where
, where 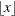 denotes the largest integer less than or equal to
denotes the largest integer less than or equal to  .
.
- number
-
specifies the fixed value of the bandwidth parameter.
The default is BANDWIDTH=ANDREWS91.
- PREWHITENING
-
specifies that prewhitening is required in the calculation.
In the calculation of the HAC estimator, the adjustment for degrees of freedom is always applied. See the section Heteroscedasticity- and Autocorrelation-Consistent Covariance Matrix Estimator for more information about the HAC estimator.
- HE
-
specifies that the errors are assumed to have heterogeneous distribution across regimes in the estimation of covariance matrix.
- HO
-
specifies that
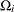 s in the calculation of confidence intervals of break dates are different across regimes.
s in the calculation of confidence intervals of break dates are different across regimes.
- HQ
-
specifies that
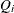 s in the calculation of confidence intervals of break dates are different across regimes.
s in the calculation of confidence intervals of break dates are different across regimes.
- HR
-
specifies that the regressors are assumed to have heterogeneous distribution across regimes in the estimation of covariance matrix.
- M=number
-
specifies the number of breaks. For a given
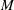 , the following tests are to be performed: (1) the
, the following tests are to be performed: (1) the 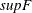 tests of no break versus the alternative hypothesis that there are
tests of no break versus the alternative hypothesis that there are 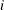 breaks,
breaks, 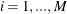 ; (2) the
; (2) the 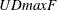 and
and 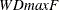 double maximum tests of no break versus the alternative hypothesis that there are unknown number of breaks up to M; and (3)
the
double maximum tests of no break versus the alternative hypothesis that there are unknown number of breaks up to M; and (3)
the 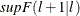 tests of
tests of 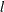 versus
versus 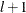 breaks,
breaks, 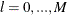 . The default is M=5.
. The default is M=5.
- NTHREADS=number
-
specifies the number of threads to be used for parallel computing. The default is the number of CPUs available.
- P=number
-
specifies the number of covariates that have coefficients unchanged over time in the partial structural change model. The first P=
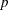 independent variables that are specified in the MODEL statement have unchanged coefficients; the rest of the independent
variables have coefficients that change across regimes. The default is P=0; i.e., the pure structural change model is estimated.
independent variables that are specified in the MODEL statement have unchanged coefficients; the rest of the independent
variables have coefficients that change across regimes. The default is P=0; i.e., the pure structural change model is estimated.
- PRINTEST=ALL | BIC | LWZ | NONE | SEQ<(number)> | number
-
specifies in which structural change models the parameter estimates are to be printed. You can specify the following option values:
- ALL
-
specifies that the parameter estimates in all structural change models with
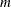 breaks,
breaks, 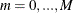 , be printed.
, be printed.
- BIC
-
specifies that the parameter estimates in the structural change model that minimizes the BIC information criterion be printed.
- LWZ
-
specifies that the parameter estimates in the structural change model that minimizes the LWZ information criterion be printed.
- NONE
-
specifies that none of the parameter estimates be printed.
- SEQ
-
specifies that the parameter estimates in the structural change model that is chosen by sequentially applying
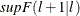 tests,
tests, 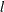 from
from 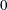 to
to 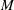 , be printed. If you specify the SEQ option, you can also specify the significance level in the parentheses, for example,
SEQ(0.10). The first
, be printed. If you specify the SEQ option, you can also specify the significance level in the parentheses, for example,
SEQ(0.10). The first 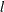 such that the p-value of
such that the p-value of 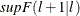 test is greater than the significance level is selected as the number of breaks in the structural change model. By default,
the significance level 5% is used for the SEQ option; i.e., specifying SEQ is equivalent to specifying SEQ(0.05).
test is greater than the significance level is selected as the number of breaks in the structural change model. By default,
the significance level 5% is used for the SEQ option; i.e., specifying SEQ is equivalent to specifying SEQ(0.05).
- number
-
specifies that the parameter estimates in the structural change model with the specified number of breaks be printed. If the specified number is greater than the number specified in the M= option, none of the parameter estimates are printed; that is, it is equivalent to specifying the NONE option.
The default is PRINTEST=ALL.
If you define the BP option without additional suboptions, all suboptions are set as default values. That is, the following two statements are equivalent:
model y = z1 z2 / BP;
model y = z1 z2 / BP=(M=5, P=0, EPS=0.05, PRINTEST=ALL);
To apply the HAC estimator with the Bartlett kernel function and print only the parameter estimates in the structural change model selected by the LWZ information criterion, you can write the SAS statement as follows:
model y = z1 z2 / BP=(HAC(KERNEL=BARTLETT), PRINTEST=LWZ);
To specify a partial structural change model, you can write the SAS statement as follows:
model y = x1 x2 x3 z1 z2 / NOINT BP=(P=3);
-
CHOW=( obs
 …obs
…obs )
)
-
computes Chow tests to evaluate the stability of the regression coefficient. The Chow test is also called the analysis-of-variance test.
Each value
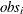 listed on the CHOW= option specifies a break point of the sample. The sample is divided into parts at the specified break
point, with observations before
listed on the CHOW= option specifies a break point of the sample. The sample is divided into parts at the specified break
point, with observations before 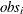 in the first part and
in the first part and 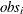 and later observations in the second part, and the fits of the model in the two parts are compared to whether both parts
of the sample are consistent with the same model.
and later observations in the second part, and the fits of the model in the two parts are compared to whether both parts
of the sample are consistent with the same model.
The break points
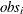 refer to observations within the time range of the dependent variable, ignoring missing values before the start of the dependent
series. Thus, CHOW=20 specifies the 20th observation after the first nonmissing observation for the dependent variable. For
example, if the dependent variable Y contains 10 missing values before the first observation with a nonmissing Y value, then
CHOW=20 actually refers to the 30th observation in the data set.
refer to observations within the time range of the dependent variable, ignoring missing values before the start of the dependent
series. Thus, CHOW=20 specifies the 20th observation after the first nonmissing observation for the dependent variable. For
example, if the dependent variable Y contains 10 missing values before the first observation with a nonmissing Y value, then
CHOW=20 actually refers to the 30th observation in the data set.
When you specify the break point, you should note the number of presample missing values.
- COEF
-
prints the transformation coefficients for the first p observations. These coefficients are formed from a scalar multiplied by the inverse of the Cholesky root of the Toeplitz matrix of autocovariances.
- CORRB
-
prints the estimated correlations of the parameter estimates.
- COVB
-
prints the estimated covariances of the parameter estimates.
- COVEST= OP | HESSIAN | QML | HC0 | HC1 | HC2 | HC3 | HC4 | HAC<(…)> | NEWEYWEST<(…)>
-
specifies the type of covariance matrix.
When COVEST=OP is specified, the outer product matrix is used to compute the covariance matrix of the parameter estimates; by default, COVEST=OP. The COVEST=HESSIAN option produces the covariance matrix by using the Hessian matrix. The quasi–maximum likelihood estimates are computed with COVEST=QML, which is equivalent to COVEST=HC0. When the final model is an OLS or AR error model, COVEST=OP, HESSIAN, or QML is ignored; the method to calculate the estimate of covariance matrix is illustrated in the section Variance Estimates and Standard Errors.
When you specify COVEST=HC
 , where
, where 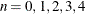 , the corresponding heteroscedasticity-consistent covariance matrix estimator (HCCME) is calculated.
, the corresponding heteroscedasticity-consistent covariance matrix estimator (HCCME) is calculated.
The HAC option specifies the heteroscedasticity- and autocorrelation-consistent (HAC) covariance matrix estimator. When you specify the HAC option, you can specify the following options in parentheses and separate them with commas:
- KERNEL=value
-
specifies the type of kernel function. You can specify the following values:
- BARTLETT
-
specifies the Bartlett kernel function.
- PARZEN
-
specifies the Parzen kernel function.
- QUADRATICSPECTRAL | QS
-
specifies the quadratic spectral kernel function.
- TRUNCATED
-
specifies the truncated kernel function.
- TUKEYHANNING | TUKEY | TH
-
specifies the Tukey-Hanning kernel function.
The default is KERNEL=QUADRATICSPECTRAL.
- KERNELLB=number
-
specifies the lower bound of the kernel weight value. Any kernel weight less than this lower bound is regarded as zero, which accelerates the calculation for big samples, especially for the quadratic spectral kernel. The default is KERNELLB=0.
- BANDWIDTH=value
-
specifies the fixed bandwidth value or bandwidth selection method to use in the kernel function. You can specify the following values:
- ANDREWS91 | ANDREWS
-
specifies the Andrews (1991) bandwidth selection method.
- NEWEYWEST94 | NW94 <(C=number)>
-
specifies the Newey and West (1994) bandwidth selection method. You can specify the C= option in the parentheses to calculate the lag selection parameter; the default is C=12.
- SAMPLESIZE | SS <(option-list)>
-
specifies that the bandwidth be calculated according to the following equation, based on the sample size:
![\[ b=\gamma T^{r} + c \]](images/etsug_autoreg0070.png)
where
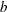 is the bandwidth parameter and
is the bandwidth parameter and 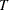 is the sample size, and
is the sample size, and 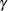 ,
,  , and
, and  are values specified by the following options within parentheses and separated by commas.
are values specified by the following options within parentheses and separated by commas.
- GAMMA=number
-
specifies the coefficient
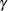 in the equation. The default is
in the equation. The default is 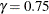 .
.
- RATE=number
-
specifies the growth rate
 in the equation. The default is
in the equation. The default is 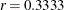 .
.
- CONSTANT=number
-
specifies the constant
 in the equation. The default is
in the equation. The default is 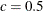 .
.
- INT
-
specifies that the bandwidth parameter must be integer; that is,
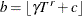 , where
, where 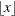 denotes the largest integer less than or equal to
denotes the largest integer less than or equal to  .
.
- number
-
specifies the fixed value of the bandwidth parameter.
The default is BANDWIDTH=ANDREWS91.
- PREWHITENING
-
specifies that prewhitening is required in the calculation.
- ADJUSTDF
-
specifies that the adjustment for degrees of freedom be required in the calculation.
The COVEST=NEWEYWEST option specifies the well-known Newey-West estimator, a special HAC estimator with (1) the Bartlett kernel; (2) the bandwidth parameter determined by the equation based on the sample size,
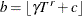 ; and (3) no adjustment for degrees of freedom and no prewhitening. By default the bandwidth parameter for Newey-West estimator
is
; and (3) no adjustment for degrees of freedom and no prewhitening. By default the bandwidth parameter for Newey-West estimator
is 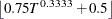 , as shown in equation (15.17) in Stock and Watson (2002). When you specify COVEST=NEWEYWEST, you can specify the following options in parentheses and separate them with commas:
, as shown in equation (15.17) in Stock and Watson (2002). When you specify COVEST=NEWEYWEST, you can specify the following options in parentheses and separate them with commas:
- GAMMA= number
-
specifies the coefficient
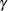 in the equation. The default is
in the equation. The default is 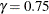 .
.
- RATE= number
-
specifies the growth rate
 in the equation. The default is
in the equation. The default is 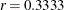 .
.
- CONSTANT= number
-
specifies the constant
 in the equation. The default is
in the equation. The default is 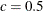 .
.
The following two statements are equivalent:
model y = x / COVEST=NEWEYWEST;
model y = x / COVEST=HAC(KERNEL=BARTLETT, BANDWIDTH=SAMPLESIZE(GAMMA=0.75, RATE=0.3333, CONSTANT=0.5, INT));Another popular sample-size-dependent bandwidth,
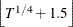 , as mentioned in Newey and West (1987), can be specified by the following statement:
, as mentioned in Newey and West (1987), can be specified by the following statement:
model y = x / COVEST=NEWEYWEST(GAMMA=1,RATE=0.25,CONSTANT=1.5);
See the section Heteroscedasticity- and Autocorrelation-Consistent Covariance Matrix Estimator for more information about HC
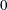 to HC
to HC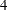 , HAC, and Newey-West estimators.
, HAC, and Newey-West estimators.
- DW=n
-
prints Durbin-Watson statistics up to the order n. The default is DW=1. When the LAGDEP option is specified, the Durbin-Watson statistic is not printed unless the DW= option is explicitly specified.
- DWPROB
-
now produces p-values for the generalized Durbin-Watson test statistics for large sample sizes. Previously, the Durbin-Watson probabilities were calculated only for small sample sizes. The new method of calculating Durbin-Watson probabilities is based on the algorithm of Ansley, Kohn, and Shively (1992).
- GINV
-
prints the inverse of the Toeplitz matrix of autocovariances for the Yule-Walker solution. See the section Computational Methods later in this chapter for more information.
-
GODFREY
GODFREY=r -
produces Godfrey’s general Lagrange multiplier test against ARMA errors.
- ITPRINT
-
prints the objective function and parameter estimates at each iteration. The objective function is the full log likelihood function for the maximum likelihood method, while the error sum of squares is produced as the objective function of unconditional least squares. For the ML method, the ITPRINT option prints the value of the full log likelihood function, not the concentrated likelihood.
-
LAGDEP
LAGDV -
prints the Durbin t statistic, which is used to detect residual autocorrelation in the presence of lagged dependent variables. See the section Generalized Durbin-Watson Tests for details.
-
LAGDEP=name
LAGDV=name -
prints the Durbin h statistic for testing the presence of first-order autocorrelation when regressors contain the lagged dependent variable whose name is specified as LAGDEP=name. If the Durbin h statistic cannot be computed, the asymptotically equivalent t statistic is printed instead. See the section Generalized Durbin-Watson Tests for details.
When the regression model contains several lags of the dependent variable, specify the lagged dependent variable for the smallest lag in the LAGDEP= option. For example:
model y = x1 x2 ylag2 ylag3 / lagdep=ylag2;
- LOGLIKL
-
prints the log likelihood value of the regression model, assuming normally distributed errors.
- NOPRINT
- NORMAL
-
specifies the Jarque-Bera’s normality test statistic for regression residuals.
- PARTIAL
-
PCHOW=( obs
 …obs
…obs )
)
-
computes the predictive Chow test. The form of the PCHOW= option is the same as the CHOW= option; see the discussion of the CHOW= option earlier in this chapter.
- RESET
-
produces Ramsey’s RESET test statistics. The RESET option tests the null model
![\[ y_{t} = \mb {x} _{t}{\beta } + u_{t} \]](images/etsug_autoreg0102.png)
against the alternative
![\[ y_{t} = \mb {x} _{t}{\beta } + \sum _{j=2}^{p}{{\phi }_{j} \hat{y}^{j}_{t}} + u_{t} \]](images/etsug_autoreg0103.png)
where
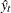 is the predicted value from the OLS estimation of the null model. The RESET option produces three RESET test statistics for
is the predicted value from the OLS estimation of the null model. The RESET option produces three RESET test statistics for
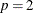 , 3, and 4.
, 3, and 4.
-
RUNS
RUNS=(Z=value) -
specifies the runs test for independence. The Z= suboption specifies the type of the time series or residuals to be tested. The values of the Z= suboption are as follows:
- Y
-
specifies the regressand. The default is Z=Y.
- RO
-
specifies the OLS residuals.
- R
-
specifies the residuals of the final model.
- RM
-
specifies the structural residuals of the final model.
- SR
-
specifies the standardized residuals of the final model, defined by residuals over the square root of the conditional variance.
-
STATIONARITY=( ADF)
STATIONARITY=( ADF=( value …value ) )
STATIONARITY=( KPSS )
STATIONARITY=( KPSS=( KERNEL=type ) )
STATIONARITY=( KPSS=( KERNEL=type TRUNCPOINTMETHOD) )
STATIONARITY=( PHILLIPS )
STATIONARITY=( PHILLIPS=( value …value ) )
STATIONARITY=( ERS)
STATIONARITY=( ERS=( value ) )
STATIONARITY=( NP)
STATIONARITY=( NP=( value ) )
STATIONARITY=( ADF<=(…)>,ERS<=(…)>, KPSS<=(…)>, NP<=(…)>, PHILLIPS<=(…)> ) -
specifies tests of stationarity or unit roots. The STATIONARITY= option provides Phillips-Perron, Phillips-Ouliaris, augmented Dickey-Fuller, Engle-Granger, KPSS, Shin, ERS, and NP tests.
The PHILLIPS or PHILLIPS= suboption of the STATIONARITY= option produces the Phillips-Perron unit root test when there are no regressors in the MODEL statement. When the model includes regressors, the PHILLIPS option produces the Phillips-Ouliaris cointegration test. The PHILLIPS option can be abbreviated as PP.
The PHILLIPS option performs the Phillips-Perron test for three null hypothesis cases: zero mean, single mean, and deterministic trend. For each case, the PHILLIPS option computes two test statistics,
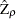 and
and 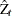 (in the original paper they are referred to as
(in the original paper they are referred to as 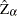 and
and 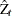 ) , and reports their p-values. These test statistics have the same limiting distributions as the corresponding Dickey-Fuller tests.
) , and reports their p-values. These test statistics have the same limiting distributions as the corresponding Dickey-Fuller tests.
The three types of the Phillips-Perron unit root test reported by the PHILLIPS option are as follows:
- Zero mean
-
computes the Phillips-Perron test statistic based on the zero mean autoregressive model:
![\[ y_{t} = {\rho }y_{t-1} + u_{t} \]](images/etsug_autoreg0109.png)
- Single mean
-
computes the Phillips-Perron test statistic based on the autoregressive model with a constant term:
![\[ y_{t} = {\mu } + {\rho }y_{t-1} + u_{t} \]](images/etsug_autoreg0110.png)
- Trend
-
computes the Phillips-Perron test statistic based on the autoregressive model with constant and time trend terms:
![\[ y_{t} = {\mu } + {\rho }y_{t-1} + {\delta }t + u_{t} \]](images/etsug_autoreg0111.png)
You can specify several truncation points
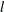 for weighted variance estimators by using the PHILLIPS=(
for weighted variance estimators by using the PHILLIPS=(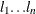 ) specification. The statistic for each truncation point
) specification. The statistic for each truncation point 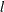 is computed as
is computed as
![\[ \sigma ^2_{Tl} = \frac{1}{T}\sum _{i=1}^{T}\hat u^2_ i + \frac{2}{T}\sum _{s=1}^{l}w_{sl} \sum _{t=s+1}^{T}\hat u_ t \hat u_{t-s} \]](images/etsug_autoreg0114.png)
where
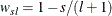 and
and 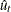 are OLS residuals. If you specify the PHILLIPS option without specifying truncation points, the default truncation point
is
are OLS residuals. If you specify the PHILLIPS option without specifying truncation points, the default truncation point
is 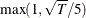 , where
, where 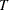 is the number of observations.
is the number of observations.
The Phillips-Perron test can be used in general time series models since its limiting distribution is derived in the context of a class of weakly dependent and heterogeneously distributed data. The marginal probability for the Phillips-Perron test is computed assuming that error disturbances are normally distributed.
When there are regressors in the MODEL statement, the PHILLIPS option computes the Phillips-Ouliaris cointegration test statistic by using the least squares residuals. The normalized cointegrating vector is estimated using OLS regression. Therefore, the cointegrating vector estimates might vary with the regressand (normalized element) unless the regression R-square is 1.
The marginal probabilities for cointegration testing are not produced. You can refer to Phillips and Ouliaris (1990) tables Ia–Ic for the
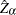 test and tables IIa–IIc for the
test and tables IIa–IIc for the 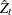 test. The standard residual-based cointegration test can be obtained using the NOINT option in the MODEL statement, while
the demeaned test is computed by including the intercept term. To obtain the demeaned and detrended cointegration tests, you
should include the time trend variable in the regressors. Refer to Phillips and Ouliaris (1990) or Hamilton (1994, Tbl. 19.1) for information about the Phillips-Ouliaris cointegration test. Note that Hamilton (1994, Tbl. 19.1) uses
test. The standard residual-based cointegration test can be obtained using the NOINT option in the MODEL statement, while
the demeaned test is computed by including the intercept term. To obtain the demeaned and detrended cointegration tests, you
should include the time trend variable in the regressors. Refer to Phillips and Ouliaris (1990) or Hamilton (1994, Tbl. 19.1) for information about the Phillips-Ouliaris cointegration test. Note that Hamilton (1994, Tbl. 19.1) uses 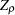 and
and 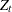 instead of the original Phillips and Ouliaris (1990) notation. We adopt the notation introduced in Hamilton. To distinguish from Student’s
instead of the original Phillips and Ouliaris (1990) notation. We adopt the notation introduced in Hamilton. To distinguish from Student’s  distribution, these two statistics are named accordingly as
distribution, these two statistics are named accordingly as 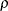 (rho) and
(rho) and  (tau).
(tau).
The ADF or ADF= suboption produces the augmented Dickey-Fuller unit root test (Dickey and Fuller, 1979). As in the Phillips-Perron test, three regression models can be specified for the null hypothesis for the augmented Dickey-Fuller test (zero mean, single mean, and trend). These models assume that the disturbances are distributed as white noise. The augmented Dickey-Fuller test can account for the serial correlation between the disturbances in some way. The model, with the time trend specification for example, is
![\[ y_{t} = {\mu } + {\rho }y_{t-1} + {\delta }t + {\gamma _1}{\Delta }y_{p-1}+\ldots +{\gamma _ p}{\Delta }y_{t-p}+ u_{t} \]](images/etsug_autoreg0125.png)
This formulation has the advantage that it can accommodate higher-order autoregressive processes in
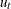 . The test statistic follows the same distribution as the Dickey-Fuller test statistic. For more information, see the section
PROBDF Function for Dickey-Fuller Tests.
. The test statistic follows the same distribution as the Dickey-Fuller test statistic. For more information, see the section
PROBDF Function for Dickey-Fuller Tests.
In the presence of regressors, the ADF option tests the cointegration relation between the dependent variable and the regressors. Following Engle and Granger (1987), a two-step estimation and testing procedure is carried out, in a fashion similar to the Phillips-Ouliaris test. The OLS residuals of the regression in the MODEL statement are used to compute the t statistic of the augmented Dickey-Fuller regression in a second step. Three cases arise based on which type of deterministic terms are included in the first step of regression. Only the constant term and linear trend cases are practically useful (Davidson and MacKinnon, 1993, page 721), and therefore are computed and reported. The test statistic, as shown in Phillips and Ouliaris (1990), follows the same distribution as the
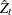 statistic in the Phillips-Ouliaris cointegration test. The asymptotic distribution is tabulated in tables IIa–IIc of Phillips
and Ouliaris (1990), and the finite sample distribution is obtained in Table 2 and Table 3 in Engle and Yoo (1987) by Monte Carlo simulation.
statistic in the Phillips-Ouliaris cointegration test. The asymptotic distribution is tabulated in tables IIa–IIc of Phillips
and Ouliaris (1990), and the finite sample distribution is obtained in Table 2 and Table 3 in Engle and Yoo (1987) by Monte Carlo simulation.
The ERS or ERS= suboption and the NP or NP= suboption provide a class of efficient unit root tests, because they reduce the size distortion and improve the power compared with traditional unit root tests such as the augmented Dickey-Fuller and Phillips-Perron tests. Two test statistics are reported with the ERS= suboption: the point optimal test and the DF-GLS test, which are originally proposed in Elliott, Rothenberg, and Stock (1996). Elliott, Rothenberg, and Stock suggest using the Schwarz Bayesian information criterion to select the optimal lag length in the augmented Dickey-Fuller regression. The maximum lag length can be specified by the ERS= suboption. The minimum lag length is 3 and the default maximum lag length is 8. Six tests, namely
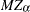 ,
, 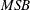 ,
, 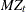 , the modified point optimal test, the point optimal test, and the DF-GLS test, discussed in Ng and Perron (2001), are reported with the NP= suboption. Ng and Perron suggest using the modified AIC to select the optimal lag length in the augmented Dickey-Fuller regression by using GLS detrended
data. The maximum lag length can be specified by the NP= suboption. The default maximum lag length is 8. The maximum lag length
in the ERS tests and Ng-Perron tests cannot exceed
, the modified point optimal test, the point optimal test, and the DF-GLS test, discussed in Ng and Perron (2001), are reported with the NP= suboption. Ng and Perron suggest using the modified AIC to select the optimal lag length in the augmented Dickey-Fuller regression by using GLS detrended
data. The maximum lag length can be specified by the NP= suboption. The default maximum lag length is 8. The maximum lag length
in the ERS tests and Ng-Perron tests cannot exceed 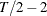 , where
, where 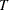 is the sample size.
is the sample size.
The KPSS, KPSS=(KERNEL=TYPE), or KPSS=(KERNEL=TYPE TRUNCPOINTMETHOD) specifications of the STATIONARITY= option produce the Kwiatkowski, Phillips, Schmidt, and Shin (1992) (KPSS) unit root test or Shin (1994) cointegration test.
Unlike the null hypothesis of the Dickey-Fuller and Phillips-Perron tests, the null hypothesis of the KPSS states that the time series is stationary. As a result, it tends to reject a random walk more often. If the model does not have an intercept, the KPSS option performs the KPSS test for three null hypothesis cases: zero mean, single mean, and deterministic trend. Otherwise, it reports the single mean and deterministic trend only. It computes a test statistic and provides tabulated critical values (Hobijn, Franses, and Ooms, 2004) for the hypothesis that the random walk component of the time series is equal to zero in the following cases (for more information, see Kwiatkowski, Phillips, Schmidt, and Shin (KPSS) Unit Root Test and Shin Cointegration Test):
- Zero mean
-
computes the KPSS test statistic based on the zero mean autoregressive model.
![\[ y_{t} = u_{t} \]](images/etsug_autoreg0131.png)
- Single mean
-
computes the KPSS test statistic based on the autoregressive model with a constant term.
![\[ y_{t} = {\mu } + u_{t} \]](images/etsug_autoreg0132.png)
- Trend
-
computes the KPSS test statistic based on the autoregressive model with constant and time trend terms.
![\[ y_{t} = {\mu } + {\delta }t + u_{t} \]](images/etsug_autoreg0133.png)
This test depends on the long-run variance of the series being defined as
![\[ \sigma ^2_{Tl} = \frac{1}{T}\sum _{i=1}^{T}\hat u^2_ i + \frac{2}{T}\sum _{s=1}^{l}w_{sl} \sum _{t=s+1}^{T}\hat u_ t \hat u_{t-s} \]](images/etsug_autoreg0114.png)
where
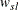 is a kernel,
is a kernel,  is a maximum lag (truncation point), and
is a maximum lag (truncation point), and 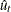 are OLS residuals or original data series. You can specify two types of the kernel:
are OLS residuals or original data series. You can specify two types of the kernel:
- KERNEL=NW | BART
-
Newey-West (or Bartlett) kernel
![\[ w(s,l)=1-\frac{s}{l+1} \]](images/etsug_autoreg0136.png)
- KERNEL=QS
-
Quadratic spectral kernel
![\[ w(s/l)=w(x)=\frac{25}{12\pi ^2 x^2}\left(\frac{\sin \left(6\pi x/5\right)}{6\pi x/5}-\cos \left(6\pi x/5\right)\right) \]](images/etsug_autoreg0137.png)
You can set the truncation point
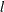 by using three different methods:
by using three different methods:
- SCHW=c
-
Schwert maximum lag formula
![\[ l=\max \left\{ 1,\textmd{floor}\left[c\left(\frac{T}{100}\right)^{1/4}\right]\right\} \]](images/etsug_autoreg0138.png)
- LAG=
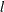
-
LAG=
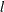 manually defined number of lags.
manually defined number of lags.
- AUTO
-
Automatic bandwidth selection (Hobijn, Franses, and Ooms, 2004) (for details, see Kwiatkowski, Phillips, Schmidt, and Shin (KPSS) Unit Root Test and Shin Cointegration Test).
If STATIONARITY=KPSS is defined without additional parameters, the Newey-West kernel is used. For the Newey-West kernel the default is the Schwert truncation point method with
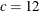 . For the quadratic spectral kernel the default is AUTO.
. For the quadratic spectral kernel the default is AUTO.
The KPSS test can be used in general time series models because its limiting distribution is derived in the context of a class of weakly dependent and heterogeneously distributed data. The limiting probability for the KPSS test is computed assuming that error disturbances are normally distributed. The p-values that are reported are based on the simulation of the limiting probability for the KPSS test.
To test for stationarity of a variable,
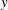 , by using default KERNEL= NW and SCHW= 12, you can use the following statements:
, by using default KERNEL= NW and SCHW= 12, you can use the following statements:
/*-- test for stationarity of regression residuals --*/ proc autoreg data=a; model y= / stationarity = (KPSS); run;
To test for stationarity of a variable,
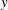 , by using quadratic spectral kernel and automatic bandwidth selection, you can use the following statements:
, by using quadratic spectral kernel and automatic bandwidth selection, you can use the following statements:
/*-- test for stationarity using quadratic spectral kernel and automatic bandwidth selection --*/ proc autoreg data=a; model y= / stationarity = (KPSS=(KERNEL=QS AUTO)); run;If there are regressors in the MODEL statement except for the intercept, the Shin (1994) cointegration test, an extension of the KPSS test, is carried out. The limiting distribution of the tests, and then the reported p-values, are different from those in the KPSS tests. See Kwiatkowski, Phillips, Schmidt, and Shin (KPSS) Unit Root Test and Shin Cointegration Test for more information.
-
TP
TP=(Z=value) -
specifies the turning point test for independence. The Z= suboption specifies the type of the time series or residuals to be tested. You can specify the following values:
- Y
-
specifies the regressand. The default is Z=Y.
- RO
-
specifies the OLS residuals.
- R
-
specifies the residuals of the final model.
- RM
-
specifies the structural residuals of the final model.
- SR
-
specifies the standardized residuals of the final model, defined by residuals over the square root of the conditional variance.
- URSQ
-
prints the uncentered regression
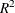 . The uncentered regression
. The uncentered regression 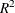 is useful to compute Lagrange multiplier test statistics, since most LM test statistics are computed as T *URSQ, where T is the number of observations used in estimation.
is useful to compute Lagrange multiplier test statistics, since most LM test statistics are computed as T *URSQ, where T is the number of observations used in estimation.
-
VNRRANK
VNRRANK=(option-list) -
specifies the rank version of the von Neumann ratio test for independence. You can specify the following options in the VNRRANK=( ) option. The options are listed within parentheses and separated by commas.
- PVALUE=DIST | SIM
-
specifies the way to calculate the p-value. By default or if PVALUE=DIST is specified, the p-value is calculated according to the asymptotic distribution of the statistic (that is, the standard normal distribution). Otherwise, for samples of size less than 100, the p-value is obtained though Monte Carlo simulation.
- Z=value
-
specifies the type of the time series or residuals to be tested. You can specify the following values:
- Y
-
specifies the regressand.
- RO
-
specifies the OLS residuals.
- R
-
specifies the residuals of the final model.
- RM
-
specifies the structural residuals of the final model.
- SR
-
specifies the standardized residuals of the final model, defined by residuals over the square root of the conditional variance.
The default is Z=Y.
Stepwise Selection Options
- BACKSTEP
-
removes insignificant autoregressive parameters. The parameters are removed in order of least significance. This backward elimination is done only once on the Yule-Walker estimates computed after the initial ordinary least squares estimation. The BACKSTEP option can be used with all estimation methods since the initial parameter values for other estimation methods are estimated using the Yule-Walker method.
- SLSTAY=value
-
specifies the significance level criterion to be used by the BACKSTEP option. The default is SLSTAY=.05.
Estimation Control Options
- CONVERGE=value
-
specifies the convergence criterion. If the maximum absolute value of the change in the autoregressive parameter estimates between iterations is less than this amount, then convergence is assumed. The default is CONVERGE=.001.
If the GARCH= option and/or the HETERO statement is specified, convergence is assumed when the absolute maximum gradient is smaller than the value specified by the CONVERGE= option or when the relative gradient is smaller than 1E–8. By default, CONVERGE=1E–5.
- INITIAL=( initial-values )
- START=( initial-values )
-
specifies initial values for some or all of the parameter estimates. The values specified are assigned to model parameters in the same order as the parameter estimates are printed in the AUTOREG procedure output. The order of values in the INITIAL= or START= option is as follows: the intercept, the regressor coefficients, the autoregressive parameters, the ARCH parameters, the GARCH parameters, the inverted degrees of freedom for Student’s t distribution, the start-up value for conditional variance, and the heteroscedasticity model parameters
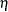 specified by the HETERO statement.
specified by the HETERO statement.
The following is an example of specifying initial values for an AR(1)-GARCH
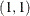 model with regressors X1 and X2:
model with regressors X1 and X2:
/*-- specifying initial values --*/ model y = w x / nlag=1 garch=(p=1,q=1) initial=(1 1 1 .5 .8 .1 .6);The model specified by this MODEL statement is
![\[ y_{t} = {\beta }_{0} + {\beta }_{1} w_{t} + {\beta }_{2} x_{t} + {\nu }_{t} \]](images/etsug_autoreg0142.png)
![\[ {\nu }_{t} = {\epsilon }_{t} - {\phi }_{1}{\nu }_{t-1} \]](images/etsug_autoreg0143.png)
![\[ {\epsilon }_{t} = \sqrt {h_{t}}e_{t} \]](images/etsug_autoreg0144.png)
![\[ h_{t} = {\omega } + {\alpha }_{1} {\epsilon }_{t-1}^{2} + {\gamma }_{1} h_{t-1} \]](images/etsug_autoreg0145.png)
![\[ {\epsilon }_{t} ~ \mr {N}(0, {\sigma }_{t}^{2}) \]](images/etsug_autoreg0146.png)
The initial values for the regression parameters, INTERCEPT (
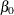 ), X1 (
), X1 (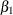 ), and X2 (
), and X2 (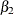 ), are specified as 1. The initial value of the AR(1) coefficient (
), are specified as 1. The initial value of the AR(1) coefficient (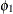 ) is specified as 0.5. The initial value of ARCH0 (
) is specified as 0.5. The initial value of ARCH0 (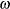 ) is 0.8, the initial value of ARCH1 (
) is 0.8, the initial value of ARCH1 (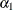 ) is 0.1, and the initial value of GARCH1 (
) is 0.1, and the initial value of GARCH1 (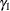 ) is 0.6.
) is 0.6.
When you use the RESTRICT statement, the initial values specified by the INITIAL= option should satisfy the restrictions specified for the parameter estimates. If they do not, the initial values you specify are adjusted to satisfy the restrictions.
- LDW
-
specifies that p-values for the Durbin-Watson test be computed using a linearized approximation of the design matrix when the model is nonlinear due to the presence of an autoregressive error process. (The Durbin-Watson tests of the OLS linear regression model residuals are not affected by the LDW option.) Refer to White (1992) for Durbin-Watson testing of nonlinear models.
- MAXITER=number
-
sets the maximum number of iterations allowed. The default is MAXITER=50. When GARCH= option in the MODEL statement and the MAXITER= option in the NLOPTIONS statement are both specified, this MAXITER= option in the MODEL statement is ignored.
- METHOD=value
-
requests the type of estimates to be computed. The values of the METHOD= option are as follows:
- METHOD=ML
-
specifies maximum likelihood estimates.
- METHOD=ULS
-
specifies unconditional least squares estimates.
- METHOD=YW
-
specifies Yule-Walker estimates.
- METHOD=ITYW
-
specifies iterative Yule-Walker estimates.
If the GARCH= or LAGDEP option is specified, the default is METHOD=ML. Otherwise, the default is METHOD=YW.
- NOMISS
-
requests the estimation to the first contiguous sequence of data with no missing values. Otherwise, all complete observations are used.
- OPTMETHOD=QN | TR
-
specifies the optimization technique when the GARCH or heteroscedasticity model is estimated. The OPTMETHOD=QN option specifies the quasi-Newton method. The OPTMETHOD=TR option specifies the trust region method. The default is OPTMETHOD=QN.