PROBDF Function for Dickey-Fuller Tests
The PROBDF function calculates significance probabilities for Dickey-Fuller tests for unit roots in time series. The PROBDF function can be used wherever SAS library functions can be used, including DATA step programs, SCL programs, and PROC MODEL programs.
Details
Theoretical Background
When a time series has a unit root, the series is nonstationary and the ordinary least squares (OLS) estimator is not normally distributed. Dickey (1976) and Dickey and Fuller (1979) studied the limiting distribution of the OLS estimator of autoregressive models for time series with a simple unit root. Dickey, Hasza, and Fuller (1984) obtained the limiting distribution for time series with seasonal unit roots. We will mainly introduce the nonseasonal tests in the following and list references for the nonseasonal tests.
Consider the Dickey-Fuller regression first. The null hypothesis is that there is an autoregressive unit root ![]() , and the alternative is
, and the alternative is ![]() , where
, where ![]() is the autoregressive coefficient of the time series
is the autoregressive coefficient of the time series
|
|
This is referred to as the zero mean (ZM) model. The standard Dickey-Fuller (DF) test assumes that errors ![]() are white noise. There are two other types of regression models that include a constant or a time trend as follows:
are white noise. There are two other types of regression models that include a constant or a time trend as follows:
|
|
|
|
|
|
These two models are referred to as the constant mean model (SM) and the trend model (TR), respectively. The constant mean
model includes a constant mean ![]() of the time series. However, the interpretation of
of the time series. However, the interpretation of ![]() depends on the stationarity in the following sense: the mean in the stationary case when
depends on the stationarity in the following sense: the mean in the stationary case when ![]() is the trend in the integrated case when
is the trend in the integrated case when ![]() . Therefore, the null hypothesis should be the joint hypothesis that
. Therefore, the null hypothesis should be the joint hypothesis that ![]() and
and ![]() . However for the unit root tests, the test statistics are concerned with the null hypothesis of
. However for the unit root tests, the test statistics are concerned with the null hypothesis of ![]() . The joint null hypothesis is not commonly used. This issue is address in Bhargava, A. (1986) with a different nesting model.
. The joint null hypothesis is not commonly used. This issue is address in Bhargava, A. (1986) with a different nesting model.
Under the null of I(1) of the Dickey-Fuller test, the differenced process is not serially correlated. There is a great need for the generalization of this specification. The augmented Dickey-Fuller (ADF) test, originally proposed in Dickey and Fuller (1979), adjusts for the serial correlation in the time series by adding lagged first differences to the autoregressive model as follows. Consider the (p +1)th order autoregressive time series
|
|
and its characteristic equation
|
|
If all the characteristic roots are less than 1 in absolute value, ![]() is stationary.
is stationary. ![]() is nonstationary if there is a unit root. If there is a unit root, the sum of the autoregressive parameters is 1, and hence
you can test for a unit root by testing whether the sum of the autoregressive parameters is 1 or not. The no-intercept model
is parameterized as
is nonstationary if there is a unit root. If there is a unit root, the sum of the autoregressive parameters is 1, and hence
you can test for a unit root by testing whether the sum of the autoregressive parameters is 1 or not. The no-intercept model
is parameterized as
|
|
where ![]() and
and
|
|
|
|
The estimators are obtained by regressing ![]() on
on ![]() . The t statistic of the ordinary least squares estimator of
. The t statistic of the ordinary least squares estimator of ![]() is the test statistic for the unit root test.
is the test statistic for the unit root test.
If the type argument value specifies a test for a nonzero mean (intercept case), the autoregressive model includes a mean term ![]() . If the type argument value specifies a test for a time trend, the model also includes a time trend term and the model is as follows:
. If the type argument value specifies a test for a time trend, the model also includes a time trend term and the model is as follows:
|
|
For testing for a seasonal unit root, consider the multiplicative model
|
|
Let ![]() . The test statistic is calculated in the following steps:
. The test statistic is calculated in the following steps:
-
Regress
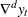 on
on 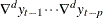 to obtain the initial estimators
to obtain the initial estimators 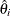 and compute residuals
and compute residuals 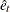 . Under the null hypothesis that
. Under the null hypothesis that 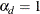 ,
, 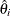 are consistent estimators of
are consistent estimators of 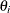 .
.
-
Regress
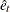 on
on 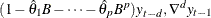 ,
,  ,
, 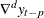 to obtain estimates of
to obtain estimates of 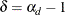 and
and 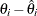 .
.
The t ratio for the estimate of ![]() produced by the second step is used as a test statistic for testing for a seasonal unit root. The estimates of
produced by the second step is used as a test statistic for testing for a seasonal unit root. The estimates of ![]() are obtained by adding the estimates of
are obtained by adding the estimates of ![]() from the second step to
from the second step to ![]() from the first step.
from the first step.
The series ![]() is assumed to be stationary, where d is the value of the third argument to the PROBDF function.
is assumed to be stationary, where d is the value of the third argument to the PROBDF function.
If the series is an ARMA process, a large value of ![]() might be desirable in order to obtain a reliable test statistic. To determine an appropriate value for
might be desirable in order to obtain a reliable test statistic. To determine an appropriate value for ![]() see Said and Dickey (1984).
see Said and Dickey (1984).
Test Statistics
The Dickey-Fuller test is used to test the null hypothesis that the time series exhibits a lag d unit root against the alternative of stationarity. The PROBDF function computes the probability of observing a test statistic more extreme than x under the assumption that the null hypothesis is true. You should reject the unit root hypothesis when PROBDF returns a small (significant) probability value.
Consider the Dickey-Fuller regression first. There are several different versions of the Dickey-Fuller test. The PROBDF function supports six versions, as selected by the type argument. Specify the type value that corresponds to the way that you calculated the test statistic x.
The last two characters of the type value specify the kind of regression model used to compute the Dickey-Fuller test statistic. The meaning of the last two characters of the type value are as follows:
- ZM
-
zero mean or no-intercept case. The test statistic x is assumed to be computed from the regression model
![\[ y_{t} = {\alpha }y_{t-1}+e_{t} \]](images/etsug_macros0096.png)
- SM
-
single mean or intercept case. The test statistic x is assumed to be computed from the regression model
![\[ y_{t} = \mu +{\alpha }y_{t-1}+e_{t} \]](images/etsug_macros0097.png)
- TR
-
intercept and deterministic time trend case. The test statistic x is assumed to be computed from the regression model
![\[ y_{t} = \mu +{\gamma } t+{\alpha }y_{t-1}+e_{t} \]](images/etsug_macros0098.png)
The first character of the type value specifies whether the regression test statistic or the studentized test statistic is used. Let ![]() be the estimated regression coefficient for the lag of the series, and let
be the estimated regression coefficient for the lag of the series, and let ![]() be the standard error of
be the standard error of ![]() . The meaning of the first character of the type value is as follows:
. The meaning of the first character of the type value is as follows:
- R
-
the regression-coefficient-based test statistic. The test statistic is
![\[ \rho = n(\hat{{\alpha }}-1) \]](images/etsug_macros0102.png)
- S
-
the studentized test statistic. The test statistic is
![\[ DF_\tau = \frac{(\hat{{\alpha }}-1)}{\mr {se}_{\hat{{\alpha }}}} \]](images/etsug_macros0103.png)
The first one is also called ![]() -test and the second is called
-test and the second is called ![]() -test. For the zero mean model, the asymptotic distributions of the Dickey-Fuller test statistics are
-test. For the zero mean model, the asymptotic distributions of the Dickey-Fuller test statistics are
|
|
|
|
|
|
For the constant mean model, the asymptotic distributions are
|
|
|
|
|
![$\displaystyle \Rightarrow \left([W(1)^2-1]/2 -W(1)\int _0^1 W(r)dr \right)\left( \int _0^1 W(r)^2 dr - \left(\int _0^1 W(r)dr \right)^2\right)^{-1/2} $](images/etsug_macros0113.png) |
For the trend model, the asymptotic distributions are
![\begin{equation*} \begin{split} n(\hat{\alpha }-1) & \Rightarrow \left[ W(r)dW +12\left(\int _0^1 rW(r)dr -\frac{1}{2}\int _0^1 W(r)dr \right) \left( \int _0^1 W(r)dr - \frac12 W(1)\right) \right. \\ & \quad \left. -W(1) \int _0^1 W(r)dr \right] D^{-1} \\ DF_\tau & \Rightarrow \left[ W(r)dW +12\left(\int _0^1 rW(r)dr -\frac{1}{2}\int _0^1 W(r)dr \right) \left( \int _0^1 W(r)dr - \frac12 W(1)\right) \right. \\ & \quad \left. -W(1) \int _0^1 W(r)dr \right] D^{1/2} \end{split}\end{equation*}](images/etsug_macros0114.png) |
where
|
|
See Dickey and Fuller (1979), Dickey, Hasza, and Fuller (1984), and Hamilton (1994) for more information about the Dickey-Fuller
test null distribution. The preceding formulas are for the basic Dickey-Fuller test. The PROBDF function can also be used
for the augmented Dickey-Fuller test, in which the error term ![]() is modeled as an autoregressive process; however, the test statistic is computed somewhat differently for the augmented Dickey-Fuller
test. For the nonseasonal augmented Dickey-Fuller test, the test statistics can take one of the two forms similar to Dickey-Fuller
test. One is the OLS
is modeled as an autoregressive process; however, the test statistic is computed somewhat differently for the augmented Dickey-Fuller
test. For the nonseasonal augmented Dickey-Fuller test, the test statistics can take one of the two forms similar to Dickey-Fuller
test. One is the OLS ![]() value
value
|
|
and the other is given by
|
|
The asymptotic distributions of the test statistics are the same as those of the standard Dickey-Fuller test statistics. See Dickey, Hasza, and Fuller (1984) and Hamilton (1994) for information about seasonal and nonseasonal augmented Dickey-Fuller tests.
The PROBDF function is calculated from approximating functions fit to empirical quantiles that are produced by a Monte Carlo
simulation that employs ![]() replications for each simulation. Separate simulations were performed for selected values of
replications for each simulation. Separate simulations were performed for selected values of ![]() and for
and for ![]() (where
(where ![]() and
and ![]() are the second and third arguments to the PROBDF function).
are the second and third arguments to the PROBDF function).
The maximum error of the PROBDF function is approximately ![]() for d in the set (1,2,4,6,12) and can be slightly larger for other d values. (Because the number of simulation replications used to produce the PROBDF function is much greater than the 60,000
replications used by Dickey and Fuller (1979) and Dickey, Hasza, and Fuller (1984), the PROBDF function can be expected to
produce results that are substantially more accurate than the critical values reported in those papers.)
for d in the set (1,2,4,6,12) and can be slightly larger for other d values. (Because the number of simulation replications used to produce the PROBDF function is much greater than the 60,000
replications used by Dickey and Fuller (1979) and Dickey, Hasza, and Fuller (1984), the PROBDF function can be expected to
produce results that are substantially more accurate than the critical values reported in those papers.)
Examples
Suppose the data set TEST contains 104 observations of the time series variable Y, and you want to test the null hypothesis that there exists a lag 4 seasonal unit root in the Y series. The following statements illustrate how to perform the single-mean Dickey-Fuller regression coefficient test using PROC REG and PROBDF.
data test1;
set test;
y4 = lag4(y);
run;
proc reg data=test1 outest=alpha;
model y = y4 / noprint;
run;
data _null_;
set alpha;
x = 100 * ( y4 - 1 );
p = probdf( x, 100, 4, "RSM" );
put p= pvalue5.3;
run;
To perform the augmented Dickey-Fuller test, regress the differences of the series on lagged differences and on the lagged value of the series, and compute the test statistic from the regression coefficient for the lagged series. The following statements illustrate how to perform the single-mean augmented Dickey-Fuller studentized test for a simple unit root using PROC REG and PROBDF:
data test1;
set test;
yl = lag(y);
yd = dif(y);
yd1 = lag1(yd); yd2 = lag2(yd);
yd3 = lag3(yd); yd4 = lag4(yd);
run;
proc reg data=test1 outest=alpha covout;
model yd = yl yd1-yd4 / noprint;
run;
data _null_;
set alpha;
retain a;
if _type_ = 'PARMS' then a = yl ;
if _type_ = 'COV' & _NAME_ = 'Y1' then do;
x = a / sqrt(yl);
p = probdf( x, 99, 1, "SSM" );
put p= pvalue5.3;
end;
run;
The %DFTEST macro provides an easier way to perform Dickey-Fuller tests. The following statements perform the same tests as the preceding example:
%dftest( test, y, ar=4 ); %put p=&dftest;