The AUTOREG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesAutoregressive Error ModelAlternative Autocorrelation Correction MethodsGARCH ModelsHeteroscedasticity- and Autocorrelation-Consistent Covariance Matrix EstimatorGoodness-of-Fit Measures and Information CriteriaTestingPredicted ValuesOUT= Data SetOUTEST= Data SetPrinted OutputODS Table NamesODS Graphics
Missing ValuesAutoregressive Error ModelAlternative Autocorrelation Correction MethodsGARCH ModelsHeteroscedasticity- and Autocorrelation-Consistent Covariance Matrix EstimatorGoodness-of-Fit Measures and Information CriteriaTestingPredicted ValuesOUT= Data SetOUTEST= Data SetPrinted OutputODS Table NamesODS Graphics -
Examples

- References
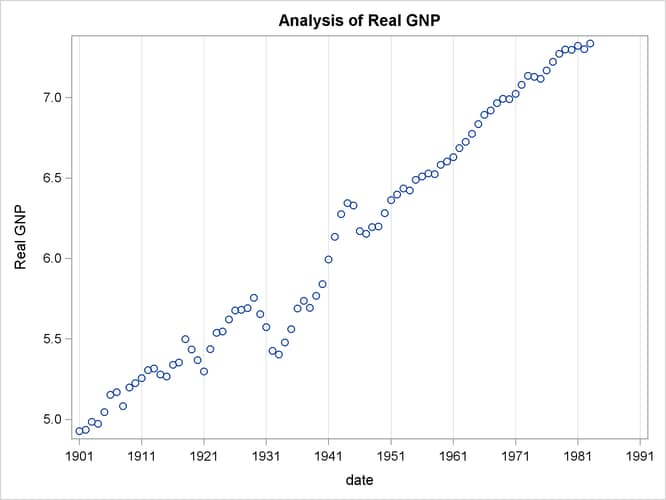
Example 8.1 Analysis of Real Output Series
In this example, the annual real output series is analyzed over the period 1901 to 1983 (Balke and Gordon, 1986, pp. 581–583). With the following DATA step, the original data are transformed using the natural logarithm, and the differenced series DY is created for further analysis. The log of real output is plotted in Output 8.1.1.
title 'Analysis of Real GNP';
data gnp;
date = intnx( 'year', '01jan1901'd, _n_-1 );
format date year4.;
input x @@;
y = log(x);
dy = dif(y);
t = _n_;
label y = 'Real GNP'
dy = 'First Difference of Y'
t = 'Time Trend';
datalines;
137.87 139.13 146.10 144.21 155.04 172.97 175.61 161.22
... more lines ...
proc sgplot data=gnp noautolegend;
scatter x=date y=y;
xaxis grid values=('01jan1901'd '01jan1911'd '01jan1921'd '01jan1931'd
'01jan1941'd '01jan1951'd '01jan1961'd '01jan1971'd
'01jan1981'd '01jan1991'd);
run;
Output 8.1.1: Real Output Series: 1901 – 1983
The (linear) trend-stationary process is estimated using the following form:
|
|
where
|
|
|
|
The preceding trend-stationary model assumes that uncertainty over future horizons is bounded since the error term, ![]() , has a finite variance. The maximum likelihood AR estimates from the statements that follow are shown in Output 8.1.2:
, has a finite variance. The maximum likelihood AR estimates from the statements that follow are shown in Output 8.1.2:
proc autoreg data=gnp; model y = t / nlag=2 method=ml; run;
Output 8.1.2: Estimating the Linear Trend Model
| Analysis of Real GNP |
| Maximum Likelihood Estimates | |||
|---|---|---|---|
| SSE | 0.23954331 | DFE | 79 |
| MSE | 0.00303 | Root MSE | 0.05507 |
| SBC | -230.39355 | AIC | -240.06891 |
| MAE | 0.04016596 | AICC | -239.55609 |
| MAPE | 0.69458594 | HQC | -236.18189 |
| Log Likelihood | 124.034454 | Regress R-Square | 0.8645 |
| Durbin-Watson | 1.9935 | Total R-Square | 0.9947 |
| Observations | 83 | ||
| Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Variable | DF | Estimate | Standard Error |
t Value | Approx Pr > |t| |
Variable Label |
| Intercept | 1 | 4.8206 | 0.0661 | 72.88 | <.0001 | |
| t | 1 | 0.0302 | 0.001346 | 22.45 | <.0001 | Time Trend |
| AR1 | 1 | -1.2041 | 0.1040 | -11.58 | <.0001 | |
| AR2 | 1 | 0.3748 | 0.1039 | 3.61 | 0.0005 | |
| Autoregressive parameters assumed given | ||||||
|---|---|---|---|---|---|---|
| Variable | DF | Estimate | Standard Error |
t Value | Approx Pr > |t| |
Variable Label |
| Intercept | 1 | 4.8206 | 0.0661 | 72.88 | <.0001 | |
| t | 1 | 0.0302 | 0.001346 | 22.45 | <.0001 | Time Trend |
Nelson and Plosser (1982) failed to reject the hypothesis that macroeconomic time series are nonstationary and have no tendency to return to a trend line. In this context, the simple random walk process can be used as an alternative process:
|
|
where ![]() and
and ![]() . In general, the difference-stationary process is written as
. In general, the difference-stationary process is written as
|
|
where ![]() is the lag operator. You can observe that the class of a difference-stationary process should have at least one unit root
in the AR polynomial
is the lag operator. You can observe that the class of a difference-stationary process should have at least one unit root
in the AR polynomial ![]() .
.
The Dickey-Fuller procedure is used to test the null hypothesis that the series has a unit root in the AR polynomial. Consider the following equation for the augmented Dickey-Fuller test:
|
|
where ![]() . The test statistic
. The test statistic ![]() is the usual t ratio for the parameter estimate
is the usual t ratio for the parameter estimate ![]() , but the
, but the ![]() does not follow a t distribution.
does not follow a t distribution.
The following code performs the augmented Dickey-Fuller test with ![]() and we are interesting in the test results in the linear time trend case since the previous plot reveals there is a linear
trend.
and we are interesting in the test results in the linear time trend case since the previous plot reveals there is a linear
trend.
proc autoreg data = gnp; model y = / stationarity =(adf =3); run;
The augmented Dickey-Fuller test indicates that the output series may have a difference-stationary process. The statistic
Tau with linear time trend has a value of ![]() and its p-value is
and its p-value is ![]() . The statistic Rho has a p-value of
. The statistic Rho has a p-value of ![]() which also indicates the null of unit root is accepted at the 5% level. (See Output 8.1.3.)
which also indicates the null of unit root is accepted at the 5% level. (See Output 8.1.3.)
Output 8.1.3: Augmented Dickey-Fuller Test Results
| Analysis of Real GNP |
| Augmented Dickey-Fuller Unit Root Tests | |||||||
|---|---|---|---|---|---|---|---|
| Type | Lags | Rho | Pr < Rho | Tau | Pr < Tau | F | Pr > F |
| Zero Mean | 3 | 0.3827 | 0.7732 | 3.3342 | 0.9997 | ||
| Single Mean | 3 | -0.1674 | 0.9465 | -0.2046 | 0.9326 | 5.7521 | 0.0211 |
| Trend | 3 | -18.0246 | 0.0817 | -2.6190 | 0.2732 | 3.4472 | 0.4957 |
The AR(1) model for the differenced series DY is estimated using the maximum likelihood method for the period 1902 to 1983. The difference-stationary process is written
|
|
|
|
The estimated value of ![]() is
is ![]() and that of
and that of ![]() is 0.0293. All estimated values are statistically significant. The PROC step follows:
is 0.0293. All estimated values are statistically significant. The PROC step follows:
proc autoreg data=gnp; model dy = / nlag=1 method=ml; run;
The printed output produced by the PROC step is shown in Output 8.1.4.
Output 8.1.4: Estimating the Differenced Series with AR(1) Error
| Analysis of Real GNP |
| Maximum Likelihood Estimates | |||
|---|---|---|---|
| SSE | 0.27107673 | DFE | 80 |
| MSE | 0.00339 | Root MSE | 0.05821 |
| SBC | -226.77848 | AIC | -231.59192 |
| MAE | 0.04333026 | AICC | -231.44002 |
| MAPE | 153.637587 | HQC | -229.65939 |
| Log Likelihood | 117.795958 | Regress R-Square | 0.0000 |
| Durbin-Watson | 1.9268 | Total R-Square | 0.0900 |
| Observations | 82 | ||
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Variable | DF | Estimate | Standard Error |
t Value | Approx Pr > |t| |
| Intercept | 1 | 0.0293 | 0.009093 | 3.22 | 0.0018 |
| AR1 | 1 | -0.2967 | 0.1067 | -2.78 | 0.0067 |
| Autoregressive parameters assumed given | |||||
|---|---|---|---|---|---|
| Variable | DF | Estimate | Standard Error |
t Value | Approx Pr > |t| |
| Intercept | 1 | 0.0293 | 0.009093 | 3.22 | 0.0018 |