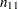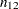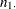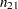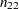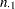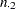The FREQ Procedure
Risks and Risk Differences
The RISKDIFF option in the TABLES statement provides estimates of risks (binomial proportions) and risk differences for 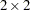 tables. This analysis might be appropriate when comparing the proportion of some characteristic for two groups, where row 1 and row 2 correspond to the two groups, and the columns correspond to two possible characteristics or outcomes. For example, the row variable might be a treatment or dose, and the column variable might be the response. See Collett (1991), Fleiss, Levin, and Paik (2003), and Stokes, Davis, and Koch (2000) for more information.
tables. This analysis might be appropriate when comparing the proportion of some characteristic for two groups, where row 1 and row 2 correspond to the two groups, and the columns correspond to two possible characteristics or outcomes. For example, the row variable might be a treatment or dose, and the column variable might be the response. See Collett (1991), Fleiss, Levin, and Paik (2003), and Stokes, Davis, and Koch (2000) for more information.
Let the frequencies of the 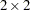 table be represented as follows.
table be represented as follows.
Column 1 |
Column 2 |
Total |
|
Row 1 |
|
|
|
Row 2 |
|
|
|
Total |
|
|
|
For column 1 and column 2, PROC FREQ provides estimates of the row 1 risk (proportion), the row 2 risk, the overall risk, and the risk difference. The risk difference is defined as the row 1 risk minus the row 2 risk. The risks are binomial proportions of their rows (row 1, row 2, or overall), and the computation of their standard errors and confidence limits follow the binomial proportion computations, which are described in the section Binomial Proportion.
The column 1 risk for row 1 is the proportion of row 1 observations classified in column 1,
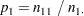 |
This estimates the conditional probability of the column 1 response, given the first level of the row variable.
The column 1 risk for row 2 is the proportion of row 2 observations classified in column 1,
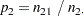 |
The overall column 1 risk is the proportion of all observations classified in column 1,
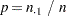 |
The column 1 risk difference compares the risks for the two rows, and it is computed as the column 1 risk for row 1 minus the column 1 risk for row 2,
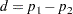 |
The risks and risk difference are defined similarly for column 2.
The standard error of the column 1 risk for row 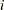 is computed as
is computed as
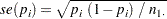 |
The standard error of the overall column 1 risk is computed as
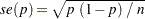 |
If the two rows represent independent binomial samples, the standard error for the column 1 risk difference is computed as
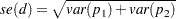 |
The standard errors are computed in a similar manner for the column 2 risks and risk difference.
Confidence Limits
By default, the RISKDIFF option provides standard Wald asymptotic confidence limits for the risks (row 1, row 2, and overall) and the risk difference. The RISKDIFF option also provides other types of confidence limits and tests for the risk difference. See the sections Risk Difference Confidence Limits and Risk Difference Tests for details.
The risks are equivalent to binomial proportions of their corresponding rows. This section describes the Wald confidence limits for risks that are provided by the RISKDIFF option. The BINOMIAL option provides additional confidence limit types and tests for risks in the binomial proportion framework. See the sections Binomial Confidence Limits and Binomial Tests for details.
The Wald asymptotic confidence limits are based on the normal approximation to the binomial distribution. PROC FREQ computes the Wald confidence limits for the risks and risk differences as
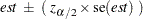 |
where  is the estimate,
is the estimate, 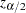 is the
is the 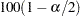 th percentile of the standard normal distribution, and
th percentile of the standard normal distribution, and  is the standard error of the estimate. The confidence level
is the standard error of the estimate. The confidence level  is determined from the value of the ALPHA= option, which, by default, equals 0.05 and produces 95% confidence limits.
is determined from the value of the ALPHA= option, which, by default, equals 0.05 and produces 95% confidence limits.
If you specify the CORRECT riskdiff-option or the RISKDIFFC option, PROC FREQ includes continuity corrections in the Wald asymptotic confidence limits for the risks and risk differences. The purpose of a continuity correction is to adjust for the difference between the normal approximation and the binomial distribution, which is discrete. See Fleiss, Levin, and Paik (2003) for more information. With the continuity correction, the asymptotic confidence limits are computed as
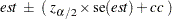 |
where 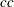 is the continuity correction. For the row 1 risk,
is the continuity correction. For the row 1 risk, 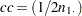 ; for the row 2 risk,
; for the row 2 risk,  ; for the overall risk,
; for the overall risk, 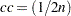 ; and for the risk difference,
; and for the risk difference,  . The column 1 and column 2 risks use the same continuity corrections.
. The column 1 and column 2 risks use the same continuity corrections.
PROC FREQ also computes exact (Clopper-Pearson) confidence limits for the column 1, column 2, and overall risks. These confidence limits are constructed by inverting the equal-tailed test based on the binomial distribution. PROC FREQ uses the  distribution to compute the Clopper-Pearson confidence limits. See the section Exact (Clopper-Pearson) Confidence Limits for details.
distribution to compute the Clopper-Pearson confidence limits. See the section Exact (Clopper-Pearson) Confidence Limits for details.
Risk Difference Confidence Limits
You can request additional confidence limits for the risk difference by specifying the CL= riskdiff-option. Available confidence limit types include exact unconditional, Farrington-Manning, Hauck-Anderson, Newcombe score, and Wald. Continuity-corrected versions of the Newcombe and Wald confidence limits are available. By default, the Wald confidence limits use a sample-based variance; alternatively, you can request a test-based variance and specify the null risk difference value.
The confidence coefficient for the confidence limits produced by the CL= riskdiff-option is 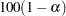 %, where the value of
%, where the value of  is determined by the ALPHA= option. By default, ALPHA=0.05, which produces 95% confidence limits. This differs from the test-based confidence limits that are provided with the equivalence, noninferiority, and superiority tests, which have a confidence coefficient of
is determined by the ALPHA= option. By default, ALPHA=0.05, which produces 95% confidence limits. This differs from the test-based confidence limits that are provided with the equivalence, noninferiority, and superiority tests, which have a confidence coefficient of 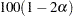 % (Schuirmann 1999). See the section Risk Difference Tests for details.
% (Schuirmann 1999). See the section Risk Difference Tests for details.
The section Exact Unconditional Confidence Limits for the Risk Difference describes the computation of the exact confidence limits. The confidence limits are constructed by inverting two separate one-sided exact tests (tail method). By default, the tests are based on the unstandardized risk difference. If you specify the RISKDIFF(METHOD=FMSCORE) option, the Farrington-Manning score is used as the test statistic.
PROC FREQ computes the Newcombe confidence limits for the risk difference as described in the subsection Newcombe Score Confidence Limits in the section Noninferiority Tests, except that the Newcombe confidence limits produced by the CL= riskdiff-option have a confidence coefficient of 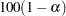 %.
%.
The following sections describe the computation of the Farrington-Manning, Hauck-Anderson, and Wald confidence limits for the risk difference.
Farrington-Manning Confidence Limits The Farrington-Manning confidence limits for the risk difference are computed as
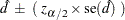 |
where 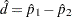 ,
, 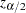 is the
is the 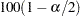 th percentile of the standard normal distribution, and the standard error is
th percentile of the standard normal distribution, and the standard error is
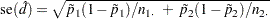 |
where  and
and 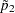 are the maximum likelihood estimators of
are the maximum likelihood estimators of 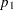 and
and 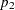 under the null hypothesis that the risk difference equals
under the null hypothesis that the risk difference equals  .
.
The subsection Farrington-Manning Test in the section Noninferiority Tests describes the computation of the maximum likelihood estimators  and
and 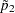 . See Farrington and Manning (1990) for details.
. See Farrington and Manning (1990) for details.
This computation uses a null hypothesis value of the risk difference, which you can specify in the CL=FM(NULL=value) riskdiff=option. By default, PROC FREQ uses a null value of 0. This differs from the Farrington-Manning confidence limits that are produced in the noninferiority analysis, where the null value of the risk difference is based on the test margin (which is specified by the MARGIN= riskdiff-option).
Hauck-Anderson Confidence Limits The Hauck-Anderson confidence limits for the risk difference are computed as
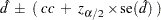 |
where 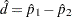 and
and 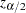 is the
is the 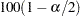 th percentile of the standard normal distribution. The standard error is computed from the sample proportions as
th percentile of the standard normal distribution. The standard error is computed from the sample proportions as
 |
The Hauck-Anderson continuity correction 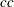 is computed as
is computed as
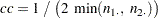 |
See Hauck and Anderson (1986) for more information. The subsection Hauck-Anderson Test in the section Noninferiority Tests describes the corresponding noninferiority test.
Wald Confidence Limits The Wald confidence limits for the risk difference are computed as
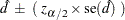 |
where 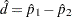 and
and 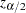 is the
is the 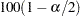 th percentile of the standard normal distribution. By default, the standard error is computed from the sample proportions as
th percentile of the standard normal distribution. By default, the standard error is computed from the sample proportions as
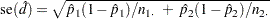 |
If you specify the CL=WALD(NULL=value) riskdiff-option, the standard error is based on the null hypothesis that the risk difference equals 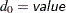 (Dunnett and Gent 1977). The standard error is computed as
(Dunnett and Gent 1977). The standard error is computed as
 |
where
 |
If you specify the CORRECT riskdiff-option, the Wald confidence limits include a continuity correction 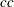 ,
,
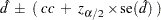 |
where 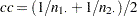 .
.
The subsection Wald Test in the section Noninferiority Tests describes the corresponding noninferiority test.
Risk Difference Tests
You can specify riskdiff-options to request tests of the risk (proportion) difference. You can request tests of equality, noninferiority, superiority, and equivalence for the risk difference. The test of equality is a standard Wald asymptotic test, available with or without a continuity correction. For noninferiority, superiority, and equivalence tests of the risk difference, the following test methods are provided: Wald (with and without continuity correction), Hauck-Anderson, Farrington-Manning, and Newcombe score (with and without continuity correction). You can specify the test method with the METHOD= riskdiff-option. By default, PROC FREQ uses METHOD=WALD.
Equality Test
If you specify the EQUAL riskdiff-option, PROC FREQ computes a test of equality, or a test of the null hypothesis that the risk difference equals zero. For the column 1 (or 2) risk difference, this test can be expressed as 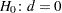 versus the alternative
versus the alternative  , where
, where  denotes the column 1 (or 2) risk difference. PROC FREQ provides a Wald asymptotic test of equality. The test statistic is computed as
denotes the column 1 (or 2) risk difference. PROC FREQ provides a Wald asymptotic test of equality. The test statistic is computed as
 |
By default, the standard error is computed from the sample proportions as
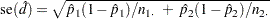 |
If you specify the VAR=NULL riskdiff-option, the standard error is based on the null hypothesis that the row 1 and row 2 risks are equal,
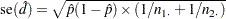 |
where 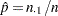 estimates the overall column 1 risk.
estimates the overall column 1 risk.
If you specify the CORRECT riskdiff-option or the RISKDIFFC option, PROC FREQ includes a continuity correction in the test statistic. If 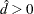 , the continuity correction is subtracted from
, the continuity correction is subtracted from 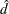 in the numerator of the test statistic; otherwise, the continuity correction is added to the numerator. The value of the continuity correction is
in the numerator of the test statistic; otherwise, the continuity correction is added to the numerator. The value of the continuity correction is 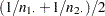 .
.
PROC FREQ computes one-sided and two-sided 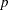 -values for this test. When the test statistic
-values for this test. When the test statistic  is greater than 0, PROC FREQ displays the right-sided p-value, which is the probability of a larger value occurring under the null hypothesis. The one-sided p-value can be expressed as
is greater than 0, PROC FREQ displays the right-sided p-value, which is the probability of a larger value occurring under the null hypothesis. The one-sided p-value can be expressed as
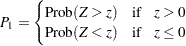 |
where 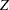 has a standard normal distribution. The two-sided p-value is computed as
has a standard normal distribution. The two-sided p-value is computed as 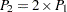 .
.
Noninferiority Tests
If you specify the NONINF riskdiff-option, PROC FREQ provides a noninferiority test for the risk difference, or the difference between two proportions. The null hypothesis for the noninferiority test is
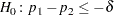 |
versus the alternative
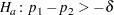 |
where 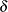 is the noninferiority margin. Rejection of the null hypothesis indicates that the row 1 risk is not inferior to the row 2 risk. See Chow, Shao, and Wang (2003) for more information.
is the noninferiority margin. Rejection of the null hypothesis indicates that the row 1 risk is not inferior to the row 2 risk. See Chow, Shao, and Wang (2003) for more information.
You can specify the value of 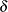 with the MARGIN= riskdiff-option. By default,
with the MARGIN= riskdiff-option. By default, 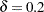 . You can specify the test method with the METHOD= riskdiff-option. The following methods are available for the risk difference noninferiority analysis: Wald (with and without continuity correction), Hauck-Anderson, Farrington-Manning, and Newcombe score (with and without continuity correction). The Wald, Hauck-Anderson, and Farrington-Manning methods provide tests and corresponding test-based confidence limits; the Newcombe score method provides only confidence limits. If you do not specify METHOD=, PROC FREQ uses the Wald test by default.
. You can specify the test method with the METHOD= riskdiff-option. The following methods are available for the risk difference noninferiority analysis: Wald (with and without continuity correction), Hauck-Anderson, Farrington-Manning, and Newcombe score (with and without continuity correction). The Wald, Hauck-Anderson, and Farrington-Manning methods provide tests and corresponding test-based confidence limits; the Newcombe score method provides only confidence limits. If you do not specify METHOD=, PROC FREQ uses the Wald test by default.
The confidence coefficient for the test-based confidence limits is 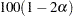 % (Schuirmann 1999). By default, if you do not specify the ALPHA= option, these are
% (Schuirmann 1999). By default, if you do not specify the ALPHA= option, these are 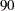 % confidence limits. You can compare the confidence limits to the noninferiority limit, –
% confidence limits. You can compare the confidence limits to the noninferiority limit, –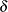 .
.
The following sections describe the noninferiority analysis methods for the risk difference.
Wald Test If you specify the METHOD=WALD riskdiff-option, PROC FREQ provides an asymptotic Wald test of noninferiority for the risk difference. This is also the default method. The Wald test statistic is computed as
 |
where (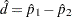 ) estimates the risk difference and
) estimates the risk difference and 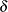 is the noninferiority margin.
is the noninferiority margin.
By default, the standard error for the Wald test is computed from the sample proportions as
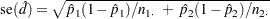 |
If you specify the VAR=NULL riskdiff-option, the standard error is based on the null hypothesis that the risk difference equals –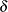 (Dunnett and Gent 1977). The standard error is computed as
(Dunnett and Gent 1977). The standard error is computed as
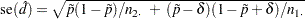 |
where
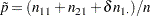 |
If you specify the CORRECT riskdiff-option or the RISKDIFFC option, a continuity correction is included in the test statistic. The continuity correction is subtracted from the numerator of the test statistic if the numerator is greater than zero; otherwise, the continuity correction is added to the numerator. The value of the continuity correction is 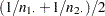 .
.
The p-value for the Wald noninferiority test is 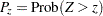 , where
, where 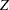 has a standard normal distribution.
has a standard normal distribution.
Hauck-Anderson Test If you specify the METHOD=HA riskdiff-option, PROC FREQ provides the Hauck-Anderson test for noninferiority. The Hauck-Anderson test statistic is computed as
 |
where 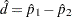 and the standard error is computed from the sample proportions as
and the standard error is computed from the sample proportions as
 |
The Hauck-Anderson continuity correction 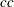 is computed as
is computed as
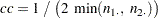 |
The p-value for the Hauck-Anderson noninferiority test is 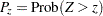 , where
, where 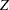 has a standard normal distribution. See Hauck and Anderson (1986) and Schuirmann (1999) for more information.
has a standard normal distribution. See Hauck and Anderson (1986) and Schuirmann (1999) for more information.
Farrington-Manning Test If you specify the METHOD=FM riskdiff-option, PROC FREQ provides the Farrington-Manning test of noninferiority for the risk difference. The Farrington-Manning test statistic is computed as
 |
where 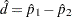 and
and
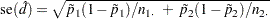 |
where  and
and 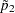 are the maximum likelihood estimators of
are the maximum likelihood estimators of 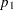 and
and 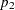 under the null hypothesis that the risk difference equals –
under the null hypothesis that the risk difference equals –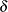 . The p-value for the Farrington-Manning noninferiority test is then
. The p-value for the Farrington-Manning noninferiority test is then 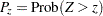 , where
, where 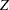 has a standard normal distribution.
has a standard normal distribution.
From Farrington and Manning (1990), the solution to the maximum likelihood equation is
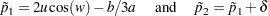 |
where
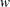 |
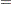 |
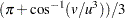 |
|||
 |
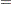 |
 |
|||
 |
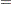 |
 |
|||
 |
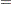 |
 |
|||
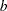 |
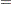 |
 |
|||
 |
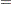 |
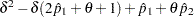 |
|||
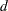 |
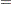 |
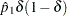 |
|||
 |
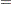 |
 |
Newcombe Score Confidence Limits If you specify the METHOD=NEWCOMBE riskdiff-option, PROC FREQ provides the Newcombe hybrid score (Wilson) confidence limits for the risk difference. The confidence coefficient for the confidence limits is 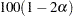 % (Schuirmann 1999). By default, if you do not specify the ALPHA= option, these are
% (Schuirmann 1999). By default, if you do not specify the ALPHA= option, these are 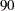 % confidence limits. You can compare the confidence limits with the noninferiority limit, –
% confidence limits. You can compare the confidence limits with the noninferiority limit, –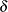 .
.
The Newcombe score confidence limits for the risk difference are constructed from the Wilson score confidence limits for each of the two individual proportions. The confidence limits for the individual proportions are used in the standard error terms of the Wald confidence limits for the proportion difference. See Newcombe (1998) and Barker et al. (2001) for more information.
Wilson score confidence limits for 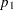 and
and 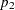 are the roots of
are the roots of
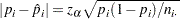 |
for  . The confidence limits are computed as
. The confidence limits are computed as
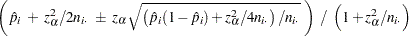 |
See the section Wilson (Score) Confidence Limits for details.
Denote the lower and upper Wilson score confidence limits for 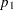 as
as 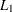 and
and 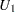 , and denote the lower and upper confidence limits for
, and denote the lower and upper confidence limits for 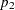 as
as  and
and 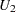 . The Newcombe score confidence limits for the proportion difference (
. The Newcombe score confidence limits for the proportion difference ( ) are computed as
) are computed as
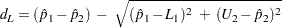 |
|||
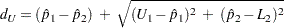 |
If you specify the CORRECT riskdiff-option, PROC FREQ provides continuity-corrected Newcombe score confidence limits. By including a continuity correction of 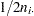 , the Wilson score confidence limits for the individual proportions are computed as the roots of
, the Wilson score confidence limits for the individual proportions are computed as the roots of
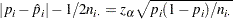 |
The continuity-corrected confidence limits for the individual proportions are then used to compute the proportion difference confidence limits 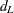 and
and 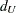 .
.
Superiority Test
If you specify the SUP riskdiff-option, PROC FREQ provides a superiority test for the risk difference. The null hypothesis is
 |
versus the alternative
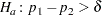 |
where 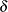 is the superiority margin. Rejection of the null hypothesis indicates that the row 1 proportion is superior to the row 2 proportion. You can specify the value of
is the superiority margin. Rejection of the null hypothesis indicates that the row 1 proportion is superior to the row 2 proportion. You can specify the value of 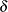 with the MARGIN= riskdiff-option. By default,
with the MARGIN= riskdiff-option. By default, 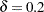 .
.
The superiority analysis is identical to the noninferiority analysis but uses a positive value of the margin 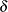 in the null hypothesis. The superiority computations follow those in the section Noninferiority Tests by replacing –
in the null hypothesis. The superiority computations follow those in the section Noninferiority Tests by replacing –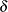 by
by 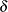 . See Chow, Shao, and Wang (2003) for more information.
. See Chow, Shao, and Wang (2003) for more information.
Equivalence Tests
If you specify the EQUIV riskdiff-option, PROC FREQ provides an equivalence test for the risk difference, or the difference between two proportions. The null hypothesis for the equivalence test is
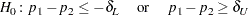 |
versus the alternative
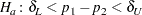 |
where 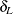 is the lower margin and
is the lower margin and 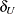 is the upper margin. Rejection of the null hypothesis indicates that the two binomial proportions are equivalent. See Chow, Shao, and Wang (2003) for more information.
is the upper margin. Rejection of the null hypothesis indicates that the two binomial proportions are equivalent. See Chow, Shao, and Wang (2003) for more information.
You can specify the value of the margins 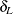 and
and  with the MARGIN= riskdiff-option. If you do not specify MARGIN=, PROC FREQ uses lower and upper margins of –0.2 and 0.2 by default. If you specify a single margin value
with the MARGIN= riskdiff-option. If you do not specify MARGIN=, PROC FREQ uses lower and upper margins of –0.2 and 0.2 by default. If you specify a single margin value 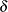 , PROC FREQ uses lower and upper margins of –
, PROC FREQ uses lower and upper margins of –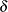 and
and 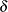 . You can specify the test method with the METHOD= riskdiff-option. The following methods are available for the risk difference equivalence analysis: Wald (with and without continuity correction), Hauck-Anderson, Farrington-Manning, and Newcombe’s score (with and without continuity correction). The Wald, Hauck-Anderson, and Farrington-Manning methods provide tests and corresponding test-based confidence limits; the Newcombe score method provides only confidence limits. If you do not specify METHOD=, PROC FREQ uses the Wald test by default.
. You can specify the test method with the METHOD= riskdiff-option. The following methods are available for the risk difference equivalence analysis: Wald (with and without continuity correction), Hauck-Anderson, Farrington-Manning, and Newcombe’s score (with and without continuity correction). The Wald, Hauck-Anderson, and Farrington-Manning methods provide tests and corresponding test-based confidence limits; the Newcombe score method provides only confidence limits. If you do not specify METHOD=, PROC FREQ uses the Wald test by default.
PROC FREQ computes two one-sided tests (TOST) for equivalence analysis (Schuirmann 1987). The TOST approach includes a right-sided test for the lower margin 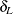 and a left-sided test for the upper margin
and a left-sided test for the upper margin 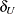 . The overall p-value is taken to be the larger of the two p-values from the lower and upper tests.
. The overall p-value is taken to be the larger of the two p-values from the lower and upper tests.
The section Noninferiority Tests gives details about the Wald, Hauck-Anderson, Farrington-Manning and Newcombe score methods for the risk difference. The lower margin equivalence test statistic takes the same form as the noninferiority test statistic but uses the lower margin value 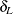 in place of –
in place of –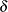 . The upper margin equivalence test statistic take the same form as the noninferiority test statistic but uses the upper margin value
. The upper margin equivalence test statistic take the same form as the noninferiority test statistic but uses the upper margin value 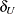 in place of –
in place of –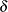 .
.
The test-based confidence limits for the risk difference are computed according to the equivalence test method that you select. If you specify METHOD=WALD with VAR=NULL, or METHOD=FM, separate standard errors are computed for the lower and upper margin tests. In this case, the test-based confidence limits are computed by using the maximum of these two standard errors. The confidence limits have a confidence coefficient of 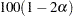 % (Schuirmann 1999). By default, if you do not specify the ALPHA= option, these are
% (Schuirmann 1999). By default, if you do not specify the ALPHA= option, these are 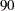 % confidence limits. You can compare the confidence limits to the equivalence limits,
% confidence limits. You can compare the confidence limits to the equivalence limits, 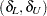 .
.
Exact Unconditional Confidence Limits for the Risk Difference
If you specify the RISKDIFF option in the EXACT statement, PROC FREQ provides exact unconditional confidence limits for the risk difference. PROC FREQ computes the confidence limits by inverting two separate one-sided tests (tail method), where the size of each test is at most 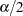 and the confidence coefficient is at least
and the confidence coefficient is at least 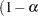 ). Exact conditional methods, described in the section Exact Statistics, do not apply to the risk difference due to the presence of a nuisance parameter (Agresti 1992). The unconditional approach eliminates the nuisance parameter by maximizing the p-value over all possible values of the parameter (Santner and Snell 1980).
). Exact conditional methods, described in the section Exact Statistics, do not apply to the risk difference due to the presence of a nuisance parameter (Agresti 1992). The unconditional approach eliminates the nuisance parameter by maximizing the p-value over all possible values of the parameter (Santner and Snell 1980).
By default, PROC FREQ uses the unstandardized risk difference as the test statistic in the confidence limit computations. If you specify the RISKDIFF(METHOD=FMSCORE) option, the procedure uses the Farrington-Manning score statistic (Chan and Zhang 1999). The score statistic is a less discrete statistic than the raw risk difference and produces less conservative confidence limits (Agresti and Min 2001). See also Santner et al. (2007) for comparisons of methods for computing exact confidence limits for the risk difference.
PROC FREQ computes the confidence limits as follows. The risk difference is defined as the difference between the row 1 and row 2 risks (proportions),  , and
, and 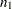 and
and 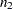 denote the row totals of the
denote the row totals of the 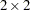 table. The joint probability function for the table can be expressed in terms of the table cell frequencies, the risk difference, and the nuisance parameter
table. The joint probability function for the table can be expressed in terms of the table cell frequencies, the risk difference, and the nuisance parameter 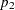 as
as
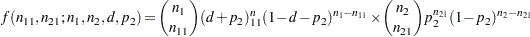 |
The 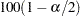 % confidence limits for the risk difference are computed as
% confidence limits for the risk difference are computed as
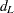 |
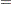 |
 |
|||
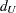 |
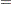 |
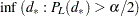 |
where
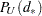 |
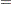 |
 |
|||
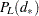 |
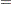 |
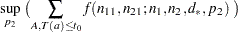 |
The set  includes all
includes all 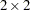 tables with row sums equal to
tables with row sums equal to 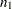 and
and 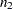 , and
, and 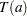 denotes the value of the test statistic for table
denotes the value of the test statistic for table  in
in 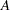 . To compute
. To compute 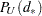 , the sum includes probabilities of those tables for which (
, the sum includes probabilities of those tables for which ( ), where
), where  is the value of the test statistic for the observed table. For a fixed value of
is the value of the test statistic for the observed table. For a fixed value of 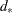 ,
, 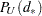 is taken to be the maximum sum over all possible values of
is taken to be the maximum sum over all possible values of 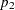 .
.
By default, PROC FREQ uses the unstandardized risk difference as the test statistic  . If you specify the RISKDIFF(METHOD=FMSCORE) option, the procedure uses the Farrington-Manning risk difference score statistic as the test statistic. The computation of the risk difference score statistic is described in the subsection Farrington-Manning Test in the section Noninferiority Tests. See Farrington and Manning (1990) and Miettinen and Nurminen (1985) for more information.
. If you specify the RISKDIFF(METHOD=FMSCORE) option, the procedure uses the Farrington-Manning risk difference score statistic as the test statistic. The computation of the risk difference score statistic is described in the subsection Farrington-Manning Test in the section Noninferiority Tests. See Farrington and Manning (1990) and Miettinen and Nurminen (1985) for more information.