The UNIVARIATE Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesRoundingDescriptive StatisticsCalculating the ModeCalculating PercentilesTests for LocationConfidence Limits for Parameters of the Normal DistributionRobust EstimatorsCreating Line Printer PlotsCreating High-Resolution GraphicsUsing the CLASS Statement to Create Comparative PlotsPositioning InsetsFormulas for Fitted Continuous DistributionsGoodness-of-Fit TestsKernel Density EstimatesConstruction of Quantile-Quantile and Probability PlotsInterpretation of Quantile-Quantile and Probability PlotsDistributions for Probability and Q-Q PlotsEstimating Shape Parameters Using Q-Q PlotsEstimating Location and Scale Parameters Using Q-Q PlotsEstimating Percentiles Using Q-Q PlotsInput Data SetsOUT= Output Data Set in the OUTPUT StatementOUTHISTOGRAM= Output Data SetOUTKERNEL= Output Data SetOUTTABLE= Output Data SetTables for Summary StatisticsODS Table NamesODS Tables for Fitted DistributionsODS GraphicsComputational Resources
Missing ValuesRoundingDescriptive StatisticsCalculating the ModeCalculating PercentilesTests for LocationConfidence Limits for Parameters of the Normal DistributionRobust EstimatorsCreating Line Printer PlotsCreating High-Resolution GraphicsUsing the CLASS Statement to Create Comparative PlotsPositioning InsetsFormulas for Fitted Continuous DistributionsGoodness-of-Fit TestsKernel Density EstimatesConstruction of Quantile-Quantile and Probability PlotsInterpretation of Quantile-Quantile and Probability PlotsDistributions for Probability and Q-Q PlotsEstimating Shape Parameters Using Q-Q PlotsEstimating Location and Scale Parameters Using Q-Q PlotsEstimating Percentiles Using Q-Q PlotsInput Data SetsOUT= Output Data Set in the OUTPUT StatementOUTHISTOGRAM= Output Data SetOUTKERNEL= Output Data SetOUTTABLE= Output Data SetTables for Summary StatisticsODS Table NamesODS Tables for Fitted DistributionsODS GraphicsComputational Resources -
Examples
 Computing Descriptive Statistics for Multiple VariablesCalculating ModesIdentifying Extreme Observations and Extreme ValuesCreating a Frequency TableCreating Basic Summary PlotsAnalyzing a Data Set With a FREQ VariableSaving Summary Statistics in an OUT= Output Data SetSaving Percentiles in an Output Data SetComputing Confidence Limits for the Mean, Standard Deviation, and VarianceComputing Confidence Limits for Quantiles and PercentilesComputing Robust EstimatesTesting for LocationPerforming a Sign Test Using Paired DataCreating a HistogramCreating a One-Way Comparative HistogramCreating a Two-Way Comparative HistogramAdding Insets with Descriptive StatisticsBinning a HistogramAdding a Normal Curve to a HistogramAdding Fitted Normal Curves to a Comparative HistogramFitting a Beta CurveFitting Lognormal, Weibull, and Gamma CurvesComputing Kernel Density EstimatesFitting a Three-Parameter Lognormal CurveAnnotating a Folded Normal CurveCreating Lognormal Probability PlotsCreating a Histogram to Display Lognormal FitCreating a Normal Quantile PlotAdding a Distribution Reference LineInterpreting a Normal Quantile PlotEstimating Three Parameters from Lognormal Quantile PlotsEstimating Percentiles from Lognormal Quantile PlotsEstimating Parameters from Lognormal Quantile PlotsComparing Weibull Quantile PlotsCreating a Cumulative Distribution PlotCreating a P-P Plot
Computing Descriptive Statistics for Multiple VariablesCalculating ModesIdentifying Extreme Observations and Extreme ValuesCreating a Frequency TableCreating Basic Summary PlotsAnalyzing a Data Set With a FREQ VariableSaving Summary Statistics in an OUT= Output Data SetSaving Percentiles in an Output Data SetComputing Confidence Limits for the Mean, Standard Deviation, and VarianceComputing Confidence Limits for Quantiles and PercentilesComputing Robust EstimatesTesting for LocationPerforming a Sign Test Using Paired DataCreating a HistogramCreating a One-Way Comparative HistogramCreating a Two-Way Comparative HistogramAdding Insets with Descriptive StatisticsBinning a HistogramAdding a Normal Curve to a HistogramAdding Fitted Normal Curves to a Comparative HistogramFitting a Beta CurveFitting Lognormal, Weibull, and Gamma CurvesComputing Kernel Density EstimatesFitting a Three-Parameter Lognormal CurveAnnotating a Folded Normal CurveCreating Lognormal Probability PlotsCreating a Histogram to Display Lognormal FitCreating a Normal Quantile PlotAdding a Distribution Reference LineInterpreting a Normal Quantile PlotEstimating Three Parameters from Lognormal Quantile PlotsEstimating Percentiles from Lognormal Quantile PlotsEstimating Parameters from Lognormal Quantile PlotsComparing Weibull Quantile PlotsCreating a Cumulative Distribution PlotCreating a P-P Plot - References
Exploring a Data Distribution
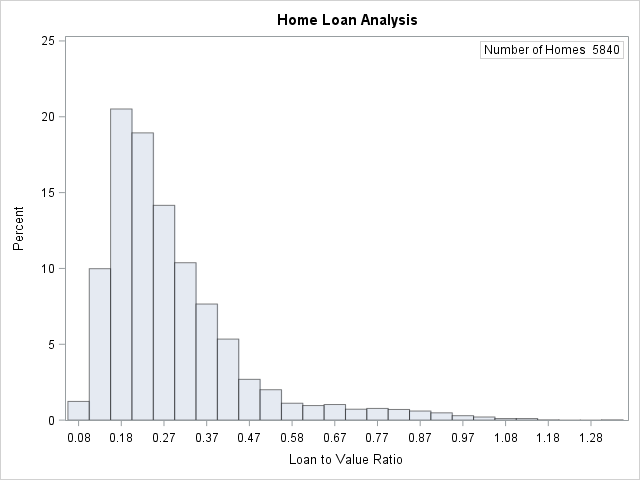
Figure 4.2 shows a histogram of the loan-to-value ratios. The histogram reveals features of the ratio distribution, such as its skewness and the peak at 0.175, which are not evident from the tables in the previous example. The following statements create the histogram:
title 'Home Loan Analysis'; ods graphics on; proc univariate data=HomeLoans noprint; histogram LoanToValueRatio / odstitle = title; inset n = 'Number of Homes' / position=ne; run;
The ODS GRAPHICS ON statement enables ODS Graphics, which causes PROC UNIVARIATE to produce ODS Graphics output. (See the section Alternatives for Producing Graphics for information about traditional graphics and ODS Graphics.)
The NOPRINT option suppresses the display of summary statistics, and the ODSTITLE= option uses the title that is specified in the SAS TITLE statement as the graph title. The INSET statement inserts the total number of analyzed home loans in the upper right (northeast) corner of the plot.
Figure 4.2: Histogram for Loan-to-Value Ratio
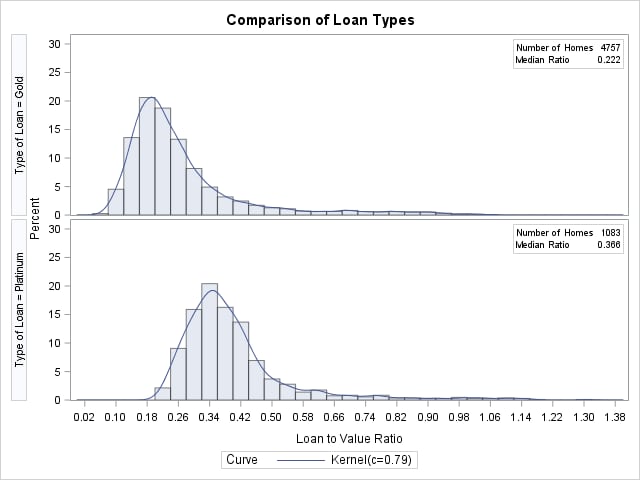
The data set HomeLoans contains a variable named LoanType that classifies the loans into two types: Gold and Platinum. It is useful to compare the distributions of LoanToValueRatio for the two types. The following statements request quantiles for each distribution and a comparative histogram, which are
shown in Figure 4.3 and Figure 4.4.
title 'Comparison of Loan Types';
ods select Histogram Quantiles;
proc univariate data=HomeLoans;
var LoanToValueRatio;
class LoanType;
histogram LoanToValueRatio / kernel
odstitle = title;
inset n='Number of Homes' median='Median Ratio' (5.3) / position=ne;
label LoanType = 'Type of Loan';
run;
options gstyle;
The ODS SELECT statement restricts the default output to the tables of quantiles and the graph produced by the HISTOGRAM statement. The CLASS statement specifies LoanType as a classification variable for the quantile computations and comparative histogram. The KERNEL option adds a smooth nonparametric estimate of the ratio density to each histogram. The INSET statement specifies summary
statistics to be displayed directly in the graph.
Figure 4.3: Quantiles for Loan-to-Value Ratio
| Comparison of Loan Types |
| Quantiles (Definition 5) | |
|---|---|
| Level | Quantile |
| 100% Max | 1.0617647 |
| 99% | 0.8974576 |
| 95% | 0.6385908 |
| 90% | 0.4471369 |
| 75% Q3 | 0.2985099 |
| 50% Median | 0.2217033 |
| 25% Q1 | 0.1734568 |
| 10% | 0.1411130 |
| 5% | 0.1213079 |
| 1% | 0.0942167 |
| 0% Min | 0.0651786 |
| Comparison of Loan Types |
| Quantiles (Definition 5) | |
|---|---|
| Level | Quantile |
| 100% Max | 1.312981 |
| 99% | 1.050000 |
| 95% | 0.691803 |
| 90% | 0.549273 |
| 75% Q3 | 0.430160 |
| 50% Median | 0.366168 |
| 25% Q1 | 0.314452 |
| 10% | 0.273670 |
| 5% | 0.253124 |
| 1% | 0.231114 |
| 0% Min | 0.215504 |
The output in Figure 4.3 shows that the median ratio for Platinum loans (0.366) is greater than the median ratio for Gold loans (0.222). The comparative histogram in Figure 4.4 enables you to compare the two distributions more easily. It shows that the ratio distributions are similar except for a shift of about 0.14.
Figure 4.4: Comparative Histogram for Loan-to-Value Ratio
A sample program for this example, univar1.sas, is available in the SAS Sample Library for Base SAS software.