The UNIVARIATE Procedure

This example shows how to display a fitted curve that is not supported by the HISTOGRAM statement. The offset of an attachment point is measured (in mm) for a number of manufactured assemblies, and the measurements (Offset) are saved in a data set named Assembly. The following statements create the data set Assembly:

data Assembly;
   label Offset = 'Offset (in mm)';
   input Offset @@;
   datalines;
11.11 13.07 11.42  3.92 11.08  5.40 11.22 14.69  6.27  9.76
 9.18  5.07  3.51 16.65 14.10  9.69 16.61  5.67  2.89  8.13
 9.97  3.28 13.03 13.78  3.13  9.53  4.58  7.94 13.51 11.43
11.98  3.90  7.67  4.32 12.69  6.17 11.48  2.82 20.42  1.01
 3.18  6.02  6.63  1.72  2.42 11.32 16.49  1.22  9.13  3.34
 1.29  1.70  0.65  2.62  2.04 11.08 18.85 11.94  8.34  2.07
 0.31  8.91 13.62 14.94  4.83 16.84  7.09  3.37  0.49 15.19
 5.16  4.14  1.92 12.70  1.97  2.10  9.38  3.18  4.18  7.22
15.84 10.85  2.35  1.93  9.19  1.39 11.40 12.20 16.07  9.23
 0.05  2.15  1.95  4.39  0.48 10.16  4.81  8.28  5.68 22.81
 0.23  0.38 12.71  0.06 10.11 18.38  5.53  9.36  9.32  3.63
12.93 10.39  2.05 15.49  8.12  9.52  7.77 10.70  6.37  1.91
 8.60 22.22  1.74  5.84 12.90 13.06  5.08  2.09  6.41  1.40
15.60  2.36  3.97  6.17  0.62  8.56  9.36 10.19  7.16  2.37
12.91  0.95  0.89  3.82  7.86  5.33 12.92  2.64  7.92 14.06
;

It is decided to fit a folded normal distribution to the offset measurements. A variable X has a folded normal distribution if , where Y is distributed as . The fitted density is

where .

You can use SAS/IML to compute preliminary estimates of and based on a method of moments given by Elandt (1961). These estimates are computed by solving equation (19) Elandt (1961), which is given by

where is the standard normal distribution function and

Then the estimates of and are given by

Begin by using PROC MEANS to compute the first and second moments and by using the following DATA step to compute the constant A:

proc means data = Assembly noprint;
   var Offset;
   output out=stat mean=m1 var=var n=n min = min;
run;

* Compute constant A from equation (19) of Elandt (1961);
data stat;
   keep m2 a min;
   set stat;
   a  = (m1*m1);
   m2 = ((n-1)/n)*var + a;
   a  = a/m2;
run;

Next, use the SAS/IML subroutine NLPDD to solve equation (19) by minimizing , and compute and :

proc iml;
   use stat;
   read all var {m2}  into m2;
   read all var {a}   into a;
   read all var {min} into min;

   * f(t) is the function in equation (19) of Elandt (1961);
   start f(t) global(a);
     y = .39894*exp(-0.5*t*t);
     y = (2*y-(t*(1-2*probnorm(t))))**2/(1+t*t);
     y = (y-a)**2;
     return(y);
   finish;

   * Minimize (f(t)-A)**2 and estimate mu and sigma;
   if ( min < 0 ) then do;
      print "Warning: Observations are not all nonnegative.";
      print "     The folded normal is inappropriate.";
      stop;
      end;
   if ( a < 0.637 ) then do;
      print "Warning: the folded normal may be inappropriate";
      end;
   opt = { 0 0 };
   con = { 1e-6 };
   x0  = { 2.0 };
   tc  = { . . . . . 1e-8 . . . . . . .};
   call nlpdd(rc,etheta0,"f",x0,opt,con,tc);
   esig0 = sqrt(m2/(1+etheta0*etheta0));
   emu0  = etheta0*esig0;

   create prelim var {emu0 esig0 etheta0};
   append;
   close prelim;

   * Define the log likelihood of the folded normal;
   start g(p) global(x);
      y = 0.0;
      do i = 1 to nrow(x);
         z = exp( (-0.5/p[2])*(x[i]-p[1])*(x[i]-p[1]) );
         z = z + exp( (-0.5/p[2])*(x[i]+p[1])*(x[i]+p[1]) );
         y = y + log(z);
      end;
      y = y - nrow(x)*log( sqrt( p[2] ) );
      return(y);
   finish;
   * Maximize the log likelihood with subroutine NLPDD;
   use assembly;
   read all var {offset} into x;
   esig0sq = esig0*esig0;
   x0      = emu0||esig0sq;
   opt     = { 1 0 };
   con     = { . 0.0, .  .  };
   call nlpdd(rc,xr,"g",x0,opt,con);
   emu     = xr[1];
   esig    = sqrt(xr[2]);
   etheta  = emu/esig;
   create parmest var{emu esig etheta};
   append;
   close parmest;
quit;

The preliminary estimates are saved in the data set Prelim, as shown in Output 4.25.1.

Now, using and as initial estimates, call the NLPDD subroutine to maximize the log likelihood, , of the folded normal distribution, where, up to a constant,

* Define the log likelihood of the folded normal;
start g(p) global(x);
   y = 0.0;
   do i = 1 to nrow(x);
      z = exp( (-0.5/p[2])*(x[i]-p[1])*(x[i]-p[1]) );
      z = z + exp( (-0.5/p[2])*(x[i]+p[1])*(x[i]+p[1]) );
      y = y + log(z);
   end;
   y = y - nrow(x)*log( sqrt( p[2] ) );
   return(y);
finish;
* Maximize the log likelihood with subroutine NLPDD;
use assembly;
read all var {offset} into x;
esig0sq = esig0*esig0;
x0      = emu0||esig0sq;
opt     = { 1 0 };
con     = { . 0.0, .  .  };
call nlpdd(rc,xr,"g",x0,opt,con);
emu     = xr[1];
esig    = sqrt(xr[2]);
etheta  = emu/esig;
create parmest var{emu esig etheta};
append;
close parmest;
quit;

The data set ParmEst contains the maximum likelihood estimates and (as well as ), as shown in Output 4.25.2.

To annotate the curve on a histogram, begin by computing the width and endpoints of the histogram intervals. The following statements save these values in a data set called OutCalc. Note that a plot is not produced at this point.

proc univariate data = Assembly noprint;
   histogram Offset / outhistogram = out normal(noprint) noplot;
run;

data OutCalc (drop = _MIDPT_);
   set out (keep = _MIDPT_) end = eof;
   retain _MIDPT1_ _WIDTH_;
   if _N_ = 1 then _MIDPT1_ = _MIDPT_;
   if eof then do;
      _MIDPTN_ = _MIDPT_;
      _WIDTH_ = (_MIDPTN_ - _MIDPT1_) / (_N_ - 1);
      output;
   end;
run;

Output 4.25.3 provides a listing of the data set OutCalc. The width of the histogram bars is saved as the value of the variable _WIDTH_; the midpoints of the first and last histogram bars are saved as the values of the variables _MIDPT1_ and _MIDPTN_.

The following statements create an annotate data set named Anno, which contains the coordinates of the fitted curve:

data Anno;
   merge ParmEst OutCalc;
   length function color $ 8;
   function = 'point';
   color    = 'black';
   size     =  2;
   xsys     = '2';
   ysys     = '2';
   when     = 'a';
   constant = 39.894*_width_;;
   left     =  _midpt1_ - .5*_width_;
   right    =  _midptn_ + .5*_width_;
   inc      = (right-left)/100;
   do x = left to right by inc;
      z1 = (x-emu)/esig;
      z2 = (x+emu)/esig;
      y  = (constant/esig)*(exp(-0.5*z1*z1)+exp(-0.5*z2*z2));
      output;
      function = 'draw';
   end;
run;

The following statements read the ANNOTATE= data set and display the histogram and fitted curve:

title 'Folded Normal Distribution';
ods graphics off;
proc univariate data=assembly noprint;
   histogram Offset / annotate = anno;
run;

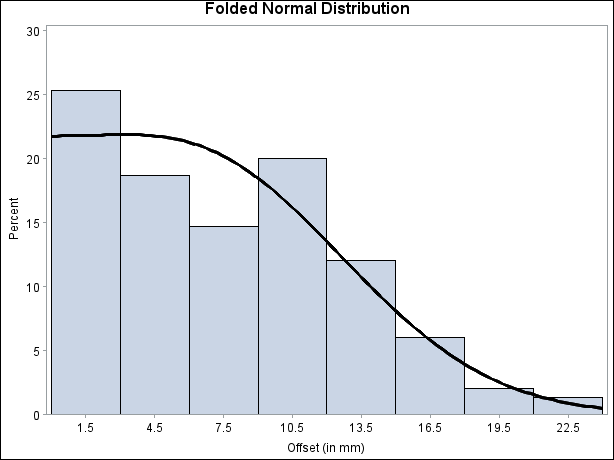
Output 4.25.4 displays the histogram and fitted curve.

A sample program for this example, uniex15.sas, is available in the SAS Sample Library for Base SAS software.