The SSM Procedure

It often happens that the transition matrix 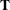(or 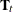in the time-varying case) specified in a STATE statement is sparse—that is, many of its elements are zero. The algorithms in the SSM procedure exploit this sparsity for computational efficiency. In most cases the sparsity of a T-block can be inferred from the context. However, if the elements of the T-block are supplied by a list of variables in parentheses, it can be difficult to recognize elements that are structurally zero (this is because of the generality of the DATA step language used for defining the variables). To simplify the specification of such sparse transition matrix, SSM procedure has adopted a convention: the variables that correspond to structural zeros can (and should) be left unset—that is, these variables are declared, but no value is assigned to them. As an example, suppose that a three-dimensional state subsection has the following form of transition matrix for some variables X1, X2, and X3 defined elsewhere in the program:

The following (incomplete) statements show how to specify such a T-block:

  array tMat{3,3};
  do i=1 to 3;
     tMat[i, i] = x1;
  end;
  tMat[2,1] = x2;
  tMat[3,1] = x3;
  state foo(3) T(g)=(tMat) ...;

In this specification only the nonzero elements of the tMat array, which contains 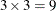elements, are assigned a value. On the other hand, the following statements show an alternate way of specifying the same T-block. This specification explicitly sets the zeros in the T-block (the elements above the diagonal and tMat[3,2]) to 0.

  array tMat{3,3};
  do i=1 to 3;
     do j=1 to 3;
         if i=j then tMat[i, j] = x1;
         else if j > i then tMat[i, j] = 0;
     end;
  end;
  tMat[2,1] = x2;
  tMat[3,1] = x3;
  tMat[3,2] = 0;
  state foo(3) T(g)=(tMat) ...;

The first specification is simpler, and is preferred. The second specification is mathematically equivalent (and generates the same output) but is computationally less efficient since its sparsity structure cannot always be reliably inferred due to the generality of the DATA step language. In the first specification, the unset elements are recognized to be structural zeros while the set elements are treated as nonzero for sparsity purposes. See Example 34.5 for a simple illustration. Proper sparsity specification can lead to significant computational savings for larger matrices.