The SSM Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 State Space Model and NotationTypes of Sequence DataOverview of Model Specification SyntaxFiltering, Smoothing, Likelihood, and Structural Break DetectionEstimation of User-Specified Linear Combination of State ElementsContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsModels with Dependent LagsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set
State Space Model and NotationTypes of Sequence DataOverview of Model Specification SyntaxFiltering, Smoothing, Likelihood, and Structural Break DetectionEstimation of User-Specified Linear Combination of State ElementsContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsModels with Dependent LagsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set -
Examples
 Bivariate Basic Structural Model Panel Data: Random-Effects and Autoregressive ModelsBackcasting, Forecasting, and InterpolationLongitudinal Data: Smoothing of Repeated MeasuresA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic Plots and Structural Break AnalysisLongitudinal Data: Variable Bandwidth SmoothingA Transfer Function Model for the Gas Furnace DataPanel Data: Dynamic Panel Model for the Cigar DataMultivariate Modeling: Long-Term Temperature TrendsBivariate Model: Sales of Mink and Muskrat FursFactor Model: Now-Casting the US EconomyLongitudinal Data: Lung Function Analysis
Bivariate Basic Structural Model Panel Data: Random-Effects and Autoregressive ModelsBackcasting, Forecasting, and InterpolationLongitudinal Data: Smoothing of Repeated MeasuresA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic Plots and Structural Break AnalysisLongitudinal Data: Variable Bandwidth SmoothingA Transfer Function Model for the Gas Furnace DataPanel Data: Dynamic Panel Model for the Cigar DataMultivariate Modeling: Long-Term Temperature TrendsBivariate Model: Sales of Mink and Muskrat FursFactor Model: Now-Casting the US EconomyLongitudinal Data: Lung Function Analysis - References
Example 34.2 Panel Data: Random-Effects and Autoregressive Models
This example shows how you can use the SSM procedure to specify and fit the two-way random-effects model and the autoregressive model to analyze a panel of time series. The fitting of dynamic panel model for such data is illustrated in Example 34.11. These (and a few other) model types can also be fitted by the PANEL procedure, a SAS/ETS procedure that is specially designed to efficiently handle the cross-sectional time series data. However, because of the differences in their model fitting algorithms, generally the parameter estimates and other fit statistics produced by the SSM and PANEL procedures do not match. The SSM procedure always uses the (restricted) maximum likelihood for parameter estimation. The estimation method used by the PANEL procedure depends on the model type and the particular estimation options.
The cross-sectional data, Cigar, that are used in the section Getting Started: SSM Procedure are reused in this example. The output shown here is less extensive than the output shown in that section. The main emphasis
of this example is how you can specify the two-way random effects model and the autoregressive model in the SSM procedure.
According to the two-way random effects model, the cigarette sales, lsales, can be described by the following equation:
![\[ \mb{lsales}_{i,t} = \pmb {\mu } + \mb{lprice} \; \pmb {\beta }_{1} + \mb{lndi} \; \pmb {\beta }_{2} + \mb{lpimin} \; \pmb {\beta }_{3} + \pmb {\zeta }_{i} + \pmb {\eta }_{t} + \pmb {\epsilon }_{i,t} \]](images/etsug_ssm0523.png)
This model represents lsales in region i and in year t as a sum of an overall intercept 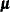 , the regression effects due to
, the regression effects due to lprice, lndi, and lpimin, a zero-mean, random effect  associated with region i, a zero-mean, random effect
associated with region i, a zero-mean, random effect 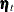 associated with year t, and the observation noise
associated with year t, and the observation noise 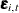 . The region-specific random effects
. The region-specific random effects  and the year-specific random effects
and the year-specific random effects 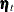 are assumed to be independent, Gaussian sequences with variances
are assumed to be independent, Gaussian sequences with variances  and
and  , respectively. In addition, they are assumed to be independent of the observation noise, which is also assumed to be a sequence
of independent, zero-mean, Gaussian variables with variance
, respectively. In addition, they are assumed to be independent of the observation noise, which is also assumed to be a sequence
of independent, zero-mean, Gaussian variables with variance  .
.
You can specify and fit this model by using the following statements:
proc ssm data=Cigar;
id year interval=year;
parms s2g/ lower=(1.e-6);
array RegionArray{46} region1-region46;
do i=1 to 46;
RegionArray[i] = (region=i);
end;
/* region-specific random effects */
state zeta(46) T(I) cov1(I)=(s2g);
component regionEffect = zeta * (RegionArray);
/* year-specific random effect */
state eta(1) type=wn cov(D);
component timeEffect = eta[1];
irregular wn;
intercept = 1.0;
model lsales = intercept lprice lndi lpimin
timeEffect regionEffect wn;
run;
The PARMS statement defines s2g, a parameter that is restricted to be positive and is used later as the variance parameter for the region effect. Similarly
the 46-dimensional array, RegionArray, of region-specific dummy variables is defined to be used later. The state subsection zeta corresponds to 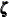 , which is the 46-dimensional vector of region-specific, zero-mean, random effects. The component
, which is the 46-dimensional vector of region-specific, zero-mean, random effects. The component regionEffect extracts the proper element of  by using the array
by using the array RegionArray. A constant column, intercept, is defined to be used later as an intercept term. The component timeEffect corresponds to 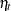 , and
, and wn specifies the observation noise  . Finally the MODEL statement defines the model. Some of the tables that are produced by running these statements are shown
in Output 34.2.1 through Output 34.2.5.
. Finally the MODEL statement defines the model. Some of the tables that are produced by running these statements are shown
in Output 34.2.1 through Output 34.2.5.
The model summary, shown in Output 34.2.1, shows that the model is defined by one MODEL statement, the dimension of the underlying state vector is 47 (because 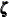 is 46-dimensional and
is 46-dimensional and 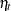 is one-dimensional), the diffuse dimension is 4 (because of the four predictors in the model), and there are three parameters
to be estimated.
is one-dimensional), the diffuse dimension is 4 (because of the four predictors in the model), and there are three parameters
to be estimated.
Output 34.2.1: Two-Way Random-Effects Model: Model Summary
Output 34.2.2 provides the likelihood information about the fitted model.
Output 34.2.2: Two-Way Random-Effects Model: Likelihood Summary
Output 34.2.3 shows the regression estimates.
Output 34.2.3: Two-Way Random-Effects Model: Regression Estimates
The ML estimate of s2g, a parameter specified in the PARMS statement, is shown in Output 34.2.4. It corresponds to  , the variance of the region effect.
, the variance of the region effect.
Output 34.2.4: Two-Way Random-Effects Model: Estimate of 
Output 34.2.5: Variance Estimates of 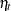 and
and 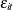
The estimates of the other unknown parameters in the model are shown in Output 34.2.5. It shows the estimate of the variance of the irregular component wn and the estimate of the variance of the time effect 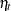 .
.
The remainder of this example describes how you can specify and fit the following first-order vector autoregessive model to the cigarette data:
![\begin{eqnarray*} \mb{lsales}_{i,t} & = & \pmb {\mu } + \mb{lprice} \; \pmb {\beta }_{1} + \mb{lndi} \; \pmb {\beta }_{2} + \mb{lpimin} \; \pmb {\beta }_{3} + \pmb {\zeta }_{t}[i] \nonumber \\ \pmb {\zeta }_{t} & = & \pmb {\Phi } \; \pmb {\zeta }_{t-1} + \pmb {\eta }_{t} \nonumber \end{eqnarray*}](images/etsug_ssm0533.png)
This model represents lsales in region i and in year t as a sum of an overall intercept 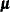 , the regression effects due to
, the regression effects due to lprice, lndi, and lpimin, and the ith element of a vector error term ![$\pmb {\zeta }_{t}[i]$](images/etsug_ssm0534.png) . The multidimensional error sequence
. The multidimensional error sequence 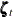 is assumed to follow a first-order autoregression with a diagonal autoregressive coefficient matrix
is assumed to follow a first-order autoregression with a diagonal autoregressive coefficient matrix 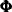 and with a multivariate, white noise sequence
and with a multivariate, white noise sequence 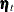 as its disturbance sequence. The covariance matrix of
as its disturbance sequence. The covariance matrix of 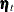 ,
, 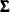 , is assumed to be dense. Note that the dimension of the vectors
, is assumed to be dense. Note that the dimension of the vectors 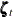 is the same as the number of cross-sections in the study (the number of regions in this example). Therefore, even for a relatively
modest panel study, the total number of parameters to be estimated can get quite large. Therefore, in this example only the
first three regions are considered in the analysis. The following statements specify and fit this model to the
is the same as the number of cross-sections in the study (the number of regions in this example). Therefore, even for a relatively
modest panel study, the total number of parameters to be estimated can get quite large. Therefore, in this example only the
first three regions are considered in the analysis. The following statements specify and fit this model to the Cigar data set:
proc ssm data=Cigar;
where region <= 3;
id year interval=year;
array RegionArray{3} region1-region3;
do i=1 to 3;
RegionArray[i] = (region=i);
end;
state zeta(3) type=varma(p(d)=1) cov(g) print=(ar cov);
component eta = zeta*(RegionArray);
intercept = 1.0;
model lsales = intercept lprice lndi lpimin eta;
run;
The vectors 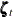 are specified in the STATE statement. The TYPE= specification signifies that the three-dimensional state subsection,
are specified in the STATE statement. The TYPE= specification signifies that the three-dimensional state subsection, zeta, follows a vector AR(1) model with a diagonal transition matrix and a disturbance covariance of a general form. The PRINT=(AR
COV) option causes the SSM procedure to print the estimated AR coefficient matrix, 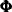 , and the disturbance error covariance
, and the disturbance error covariance 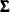 , respectively. The COMPONENT statement defines the appropriate error contribution (named
, respectively. The COMPONENT statement defines the appropriate error contribution (named eta), ![$\pmb {\zeta }_{t}[i]$](images/etsug_ssm0534.png) . Output 34.2.6 shows the estimated regression coefficients, Output 34.2.7 shows the estimate of
. Output 34.2.6 shows the estimated regression coefficients, Output 34.2.7 shows the estimate of 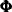 , and Output 34.2.8 shows the estimate of
, and Output 34.2.8 shows the estimate of 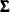 :
:
Output 34.2.6: Autoregressive Model: Regression Estimates
Output 34.2.7: Estimate of the AR Coefficient 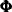
Output 34.2.8: Estimate of the Disturbance Covariance