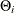The SSM Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 State Space Model and NotationTypes of Sequence DataOverview of Model Specification SyntaxFiltering, Smoothing, Likelihood, and Structural Break DetectionEstimation of User-Specified Linear Combination of State ElementsContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsModels with Dependent LagsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set
State Space Model and NotationTypes of Sequence DataOverview of Model Specification SyntaxFiltering, Smoothing, Likelihood, and Structural Break DetectionEstimation of User-Specified Linear Combination of State ElementsContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsModels with Dependent LagsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set -
Examples
 Bivariate Basic Structural Model Panel Data: Random-Effects and Autoregressive ModelsBackcasting, Forecasting, and InterpolationLongitudinal Data: Smoothing of Repeated MeasuresA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic Plots and Structural Break AnalysisLongitudinal Data: Variable Bandwidth SmoothingA Transfer Function Model for the Gas Furnace DataPanel Data: Dynamic Panel Model for the Cigar DataMultivariate Modeling: Long-Term Temperature TrendsBivariate Model: Sales of Mink and Muskrat FursFactor Model: Now-Casting the US EconomyLongitudinal Data: Lung Function Analysis
Bivariate Basic Structural Model Panel Data: Random-Effects and Autoregressive ModelsBackcasting, Forecasting, and InterpolationLongitudinal Data: Smoothing of Repeated MeasuresA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic Plots and Structural Break AnalysisLongitudinal Data: Variable Bandwidth SmoothingA Transfer Function Model for the Gas Furnace DataPanel Data: Dynamic Panel Model for the Cigar DataMultivariate Modeling: Long-Term Temperature TrendsBivariate Model: Sales of Mink and Muskrat FursFactor Model: Now-Casting the US EconomyLongitudinal Data: Lung Function Analysis - References
TREND Statement
-
TREND
name( type ) <options>;
The TREND statement defines a term in the model that follows a stochastic pattern of a certain predefined type. The options in the TREND statement enable you to specify a wide variety of commonly used stochastic patterns. Each TREND statement in effect stands for a special pair of STATE and COMPONENT statements. You can specify more than one TREND statement. Each separate TREND statement defines a component that is assumed to be independent of all other component specifications in the model. Very often the TREND statement is used to specify a component that captures the time-varying level of the data. However, in many cases it is also used to define components of a more general nature; for example, it can be used to define a noise component that follows a stationary ARMA model.
You can refer to the state that is associated with a TREND statement by appending the string "_state_" to the end of its name.
For example, name_state_ is the state that is associated with a trend named name. You can use name_state_ in a COMPONENT
statement to define a linear combination of its elements. The estimate of this linear combination can then be printed or
output to a data set. The nominal dimension of name_state_ is taken to be 1, or the number of variables in the list that is specified in the CROSS=
option in the TREND statement that is used to define name (see Example 34.4 for an example of such use of the COMPONENT statement).
Some of these trend specifications are applicable to all the data types—that is, they can be used for both regular data types and irregular data types, whereas the others require that the data be regular or regular with replication. Of course, the trend specification is only part of the overall model specification. Therefore, the other parts of the model can imply additional constraints on the data type.
Table 34.3 lists the available trend models and their data requirements. The type column shows the admissible keywords that signify the particular trend type. For brevity, the Data Type column groups the data types regular and regular with replication into one category: regular. For more information about these trend models, see the section Predefined Trend Models.
Table 34.3: Summary of Trend Types
|
type |
Data Type |
Description |
Parameters |
|---|---|---|---|
|
ARIMA(P=integer D=integer …) |
Regular |
ARIMA model specification |
AR and MA coefficients, |
|
and the error variance |
|||
|
DLL |
Regular |
Damped local linear |
Level and slope |
|
damping factor |
|||
|
LL |
Regular |
Local linear |
Level and slope |
|
RW |
Regular |
Random walk |
Level |
|
DECAY |
Irregular |
A type of decay pattern |
Level |
|
DECAY(OU) |
Irregular |
Ornstein-Uhlenbeck decay pattern |
Level |
|
GROWTH |
Irregular |
A type of growth pattern |
Level |
|
GROWTH(OU) |
Irregular |
Ornstein-Uhlenbeck growth pattern |
Level |
|
PS(order) |
Irregular |
Polynomial spline of a given order |
Level |
The keyword specification of different trend types, except possibly the ARIMA trend, is quite simple. For example, the following
statement specifies polySpline as a trend of the type second-order polynomial spline:
trend polySpline(ps(2));
Similarly, the following statement defines dampedTrend as a damped local linear trend:
trend dampedTrend(dll) slopevar=x;
The variance parameter that governs the slope equation of this trend type is given by a variable x, which must be defined elsewhere in the program. The other parameters that define dampedTrend are left unspecified (and are estimated by using the data).
The ARIMA trend specification permits specification of trends that follow an ARIMA(p,d,q) (P,D,Q)
(P,D,Q) model. The specification of ARIMA models requires some notation, which is explained first.
model. The specification of ARIMA models requires some notation, which is explained first.
Let B denote the backshift operator—that is, for any sequence 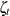 ,
, 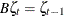 . The higher powers of B represent larger shifts (for example,
. The higher powers of B represent larger shifts (for example, 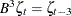 ). A random sequence
). A random sequence 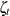 follows an ARIMA(p,d,q)
follows an ARIMA(p,d,q) (P,D,Q)
(P,D,Q) model with nonseasonal autoregressive order p, seasonal autoregressive order P, nonseasonal differencing order d, seasonal differencing order D, nonseasonal moving average order q, and seasonal moving average order Q if it satisfies the following difference equation, which is specified in terms of the polynomials in the backshift operator,
where
model with nonseasonal autoregressive order p, seasonal autoregressive order P, nonseasonal differencing order d, seasonal differencing order D, nonseasonal moving average order q, and seasonal moving average order Q if it satisfies the following difference equation, which is specified in terms of the polynomials in the backshift operator,
where 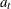 is a white noise sequence and s is the season length:
is a white noise sequence and s is the season length:
![\[ \phi (B) \Phi (B^ s) (1-B)^{d} (1 - B^{s})^{D} \zeta _ t = \theta (B) \Theta (B^ s) a_ t \]](images/etsug_ssm0061.png)
The polynomials 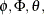 and
and 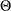 are of orders p, P, q, and Q, respectively, which can be any nonnegative integers. The season length s must be a positive integer. For example,
are of orders p, P, q, and Q, respectively, which can be any nonnegative integers. The season length s must be a positive integer. For example, 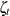 satisfies an ARIMA(1,0,1) model (that is,
satisfies an ARIMA(1,0,1) model (that is, 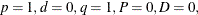 and
and 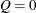 ) if
) if
![\[ \zeta _ t = \phi _{1} \zeta _{t-1} + a_ t - \theta _{1} a_{t-1} \]](images/etsug_ssm0066.png)
for some coefficients 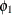 and
and 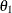 and a white noise sequence
and a white noise sequence 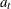 . Similarly,
. Similarly, 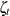 satisfies an ARIMA(0,1,1)
satisfies an ARIMA(0,1,1) (0,1,1)
(0,1,1)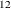 model if
model if
![\[ \zeta _ t = \zeta _{t-1} + \zeta _{t-12} - \zeta _{t-13} + a_ t - \theta _{1} a_{t-1} - \Theta _{1} a_{t-12} + \theta _{1} \Theta _{1} a_{t-13} \]](images/etsug_ssm0070.png)
for some coefficients 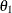 and
and 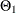 and a white noise sequence
and a white noise sequence 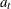 . An ARIMA process is zero-mean, stationary, and invertible if
. An ARIMA process is zero-mean, stationary, and invertible if 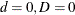 , and the defining polynomials
, and the defining polynomials 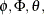 and
and 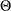 have all their roots outside the unit circle—that is, their absolute values are strictly larger than 1.0. It is assumed that
the coefficients of the polynomials
have all their roots outside the unit circle—that is, their absolute values are strictly larger than 1.0. It is assumed that
the coefficients of the polynomials 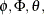 and
and 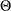 are constrained so that the stationarity and invertibility conditions are satisfied. The unknown coefficients of these polynomials
become part of the model parameter vector that is estimated by using the data. The general form of the ARIMA trend specification
is as follows:
are constrained so that the stationarity and invertibility conditions are satisfied. The unknown coefficients of these polynomials
become part of the model parameter vector that is estimated by using the data. The general form of the ARIMA trend specification
is as follows:
-
ARIMA(<P=integer> <D=integer> <Q=integer> <SP=integer> <SD=integer> <SQ=integer> <S=integer> )
By default, the different orders are equal to 0 and the season length is equal to 1. The following examples illustrate a few
different ARIMA trend specifications. The following statement defines ima as an integrated moving average trend:
trend ima(arima(d=1 q=1));
The following statement defines airTrend as a trend that satisfies the well-known airline model (ARIMA(0,1,1)(0,1,1)12 model) for monthly seasonal data:
trend airTrend(arima(d=1 q=1 sd=1 sq=1 s=12));
The following statement defines arma11 as a zero-mean ARMA(1,1) trend with autoregressive parameter fixed to 0.1:
trend arma11(arima(p=1 q=1)) ar=0.1;
For an example of the use of the ARIMA trend specification, see Example 34.6.
You can use the following options in the TREND statement to specify the trend parameters and to request printing of the trend estimates. In addition, you can create a custom combination of a given trend type by specifying the CROSS= option to create a more general trend. For an example of using the CROSS= option, see the section Getting Started: SSM Procedure and the discussion of the second model in Example 34.4. You can also check for the unexpected changes in the trend component by using the CHECKBREAK option.
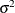
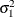
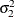

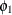
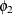
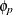
![\[ \phi (B) = 1 - \phi _1 B - \ldots - \phi _{p} B^ p \]](images/etsug_ssm0076.png)
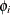
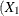
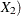
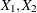
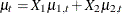
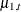
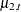
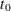
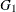
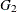
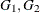
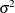
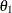
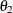
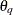
![\[ \theta (B) = 1 - \theta _1 B - \ldots - \theta _{q} B^ q \]](images/etsug_ssm0092.png)
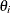
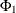
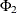
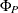
![\[ \Phi (B^ s) = 1 - \Phi _1 B^ s - \ldots - \Phi _{P} B^{s P} \]](images/etsug_ssm0097.png)
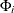
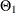
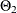
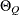
![\[ \Theta (B^ s) = 1 - \Theta _1 B^ s - \ldots - \Theta _{Q} B^{s Q} \]](images/etsug_ssm0102.png)