The SSM Procedure

Model Specification Steps

To illustrate the model specification steps, suppose y is a response variable and variables x1 and x2 are predictors. The following statements specify a model for y that includes two components named cycle and randomWalk, predictors x1 and x2, and an observation disturbance named whiteNoise:

   parms lambda / lower=(1.e-6) upper=(3.14);
   parms cycleVar / lower=(1.e-6);
   array cycleT{4} c1-c4;
   c1 = cos(lambda);
   c2 = sin(lambda);
   c3 = -c2;
   c4 = c1;
   state s_cycle(2) T(g)=(cycleT) cov(I)=(cycleVar) a1(2);
   component cycle=(1 0)*s_cycle;
   trend randomWalk(rw);
   irregular whiteNoise;
   model y = x1 x2 randomWalk cycle whiteNoise;

The specification begins with a PARMS statement that defines two parameters, lambda and cycleVar, along with their lower and upper bounds (essentially 0 and $\pi$ for lambda, and 0 and infinity for cycleVar). Next, programming statements define an array of variables, cycleT, which contains four variables, c1–c4; these variables are used later for defining the elements of the transition matrix of a state subsection. The STATE statement specifies the two-dimensional subsection s_cycle; the dimension appears within the parentheses after the name (s_cycle(2)). The T= option specifies the transition matrix for the s_cycle (T(g)=(cycleT)); the g in T(g) signifies that the form of the T matrix is general. 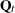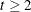The COV= option (cov(I)=(cycleVar)) specifies the covariance of the state disturbance ( $\mb{Q}_{t}$ for $t \geq 2$ ); because of the use of I in cov(I), the covariance is of the form scaled identity, essentially a two-dimensional diagonal matrix with both diagonal elements equal to cycleVar. The initial condition for s_cycle is completely diffuse because the A1= option, which specifies 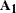$\mb{A_{1}}$ , specifies that the dimension of the diffuse vector 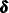$\pmb {\delta }$ is 2: a1(2). In this case there is no need to specify the covariance 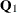$\mb{Q}_{1}$ in the initial condition. The COMPONENT statement specifies the component cycle. It specifies cycle as a dot product of two vectors—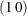 $(1 \; 0)$ and s_cycle, which merely selects the first element of s_cycle: component cycle=(1 0)*s_cycle. The TREND statement defines a component named randomWalk; its type is rw, which signifies random walk. The IRREGULAR statement defines an observation disturbance named whiteNoise. Both the randomWalk and whiteNoise specifications are only partially complete—for example, the disturbance variance of whiteNoise is not specified. These unspecified variances, trendVar, which corresponds to randomWalk, and wnVar, which corresponds to whiteNoise, are automatically included in the list of unknown parameters, 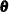$\pmb {\theta }$ , along with the parameters that are defined by the PARMS statements. Thus, the parameter vector for this model is 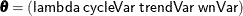$\pmb {\theta } = (\Variable{lambda} \; \Variable{cycleVar} \; \Variable{trendVar} \; \Variable{wnVar} )$ . Finally, the model specification is completed by the MODEL statement, which specifies the components of the observation equation: the response variable y, the predictors x1 and x2, the components randomWalk and cycle, and the irregular term whiteNoise.

The preceding statements result in an SSM with a three-dimensional state vector, which is the result of combining the two-dimensional state subsection, s_cycle, and a one-dimensional subsection underlying the trend, randomWalk. In this specification, the initial state is completely diffuse with 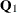$\mb{Q}_{1}$ a null matrix, and 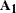$\mb{A_{1}}$ equal to the three-dimensional identity. 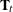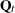The other state system matrices $\mb{T}_{t}$ and $\mb{Q}_{t}$ are time-invariant:

$\mb{T} = \left[ \begin{array}{ccc} \cos (\mr{lambda}) & \sin (\mr{lambda}) & 0 \\ -\sin (\mr{lambda}) & \cos (\mr{lambda}) & 0 \\ 0 & 0 & 1 \end{array} \right] \; \; \mb{Q} = \left[ \begin{array}{ccc} \text {cycleVar} & 0 & 0 \\ 0 & \text {cycleVar} & 0 \\ 0 & 0 & \text {trendVar} \end{array} \right]$

The observation equation is obvious with $\mb{Z} = \left[ 1 \; 0 \; 1 \right]$ .