The HETERO statement specifies variables that are related to the heteroscedasticity of the residuals and the way that these
variables are used to model the error variance. PROC HPQLIM supports the following heteroscedastic regression model:
For more information about the specification of functional forms, see the section Heteroscedasticity. The following options specify the functional forms of heteroscedasticity:
-
LINK=EXP | LINEAR
-
specifies the functional form.
-
EXP
-
specifies the exponential link function:
-
LINEAR
-
specifies the linear link function:
The default is LINK=EXP.
-
NOCONST
-
specifies that there be no constant in the linear or exponential heteroscedasticity model:
This option is ignored if you do not specify the LINK= option.
-
SQUARE
-
estimates the model by using the square of the linear heteroscedasticity function. For example, you can specify the following
heteroscedasticity function:
model y = x1 x2 / censored(lb=0);
hetero y ~ z1 / link=linear square;
The SQUARE option does not apply to the exponential heteroscedasticity function because the square of an exponential function
of  is the same as the exponential of
is the same as the exponential of  . Hence, the only difference is that all
. Hence, the only difference is that all  estimates are divided by two.
estimates are divided by two.
This option is ignored if you do not specify the LINK= option. You cannot use the HETERO statement within a Bayesian framework.
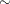 exogenous variables </ options > ;
exogenous variables </ options > ;
![\[ y_{i} = \mb{x} _{i}’{\bbeta } + {\epsilon }_{i} \]](images/etsug_hpqlim0037.png)
![\[ {\epsilon }_{i} \sim \mr{N}(0, {\sigma }_{i}^{2}) \]](images/etsug_hpqlim0038.png)




![\[ \sigma _{i}^{2} = \sigma ^2(1+(\mb{z} ^{'}_{i}{\bgamma })^{2}) \]](images/etsug_hpqlim0042.png)


