The HPPANEL Procedure

Specification Tests

The HPPANEL procedure outputs one specification test for random effects: the Hausman (1978) specification test (m statistic) can be used to test hypotheses in terms of bias or inconsistency of an estimator. This test was also proposed by Wu (1973) and further extended in Hausman and Taylor (1982). Hausman’s m statistic is as follows.

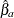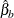Consider two estimators, ${\hat{{\beta }}_{a}}$ and ${\hat{{\beta }}_{b}}$ , which under the null hypothesis are both consistent, but only 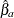${\hat{{\beta }}_{a}}$ is asymptotically efficient. Under the alternative hypothesis, only 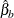${\hat{{\beta }}_{b}}$ is consistent. The m statistic is

$m = (\hat{{\beta }}_{b}- \hat{{\beta }}_{a})^{'} (\hat{\mb{S} }_{b}- \hat{\mb{S} }_{a})^{-1} (\hat{{\beta }}_{b}- \hat{{\beta }}_{a})$

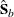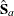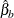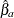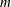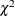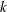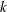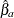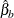where ${\hat{\mb{S} }_{b}}$ and ${\hat{\mb{S} }_{a}}$ are consistent estimates of the asymptotic covariance matrices of ${\hat{{\beta }}_{b}}$ and ${\hat{{\beta }}_{a}}$ . Then ${m}$ is distributed as ${{\chi }^{2}}$ with ${k}$ degrees of freedom, where ${k}$ is the dimension of ${\hat{{\beta }}_{a}}$ and ${\hat{{\beta }}_{b}}$ .

In the random-effects specification, the null hypothesis of no correlation between effects and regressors implies that the OLS estimates of the slope parameters are consistent and inefficient but the GLS estimates of the slope parameters are consistent and efficient. This facilitates a Hausman specification test. The reported degrees of freedom for the 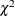${{\chi }^{2}}$ statistic are equal to the number of slope parameters. If the null hypothesis holds, the random-effects specification should be used.