The HPPANEL Procedure

Balanced Panels

Assume that the data are balanced (for example, all cross sections have T observations). Then you can write

\[ \tilde{\mi{y}}_\mi {it} = \mi{y_\mi {it}} - \bar{\mi{y}}_\mi {i \cdot } - \bar{\mi{y}}_\mi {\cdot t} + \bar{\bar{\mi{y}}} \]
\[ \tilde{\mi{\mb{x}}}_\mi {it} = \mi{\mb{x} _\mi {it}} - \bar{\mi{\mb{x}}}_\mi {i \cdot } - \bar{\mi{\mb{x}}}_\mi {\cdot t} + \bar{\bar{\mi{\mb{x}}}} \]

where the symbols are as follows:

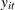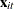  • $\mi{y_\mi {it}} $ and $\mi{\mb{x} _\mi {it}} $ are the dependent variable (a scalar) and the explanatory variables (a vector whose columns are the explanatory variables, not including a constant), respectively

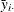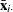  • $\bar{\mi{y}}_\mi {i \cdot } $ and $ \bar{\mi{\mb{x}}}_\mi {i \cdot }$ are cross section means

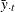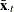  • $\bar{\mi{y}}_\mi {\cdot t} $ and $ \bar{\mi{\mb{x}}}_\mi {\cdot t}$ are time means

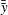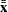  • $\bar{\bar{\mi{y}}} $ and $ \bar{\bar{\mi{\mb{x}}}}$ are the overall means

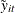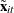The two-way fixed-effects model is simply a regression of $\tilde{\mi{y}}_\mi {it} $ on $\tilde{\mi{\mb{x}}}_\mi {it} $. Therefore, the two-way 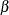${\beta }$ is given by

\[ \tilde{{\beta }}_{s}= \left(\tilde{\mi{\mb{X}}}^{'}\tilde{\mi{\mb{X}}} \right)^{-1} \tilde{\mi{\mb{X}}}^{'}\tilde{\mb{y}} \]

The following calculations of cross-sectional dummy variables, time dummy variables, and intercepts are similar to how they are calculated in the one-way model:

First, you obtain the net cross-sectional and time effects. Denote the cross-sectional effects by 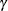$\gamma $ and the time effects by $\alpha $. These effects are calculated from the following relations:

\[ \hat{\gamma }_{i} = \left(\bar{\mi{y}}_\mi {i \cdot }- \bar{\bar{\mi{y}}} \right) - \tilde{{\beta }}_{s}\left( \bar{\mi{x}}_\mi {i \cdot }- \bar{\bar{\mi{x}}} \right) \]
\[ \hat{\alpha }_{t} = \left(\bar{\mi{y}}_{\cdot \mi{t}}- \bar{\bar{\mi{y}}} \right) - \tilde{{\beta }}_{s}\left( \bar{\mi{x}}_{\cdot \mi{t}}- \bar{\bar{\mi{x}}} \right) \]

Use the superscript C and T to denote the cross-sectional dummy variables and time dummy variables, respectively. Under the NOINT option, the following equations produce the dummy variables:

\[ D_ i^{C} = \hat{\gamma }_{i} + \hat{\alpha }_{T} \]
\[ D_ t^{T} = \hat{\alpha }_{t}- \hat{\alpha }_{T} \]

When an intercept is specified, the equations for dummy variables and intercept are

\[ D_ i^{C} = \hat{\gamma }_{i}- \hat{\gamma }_{N} \]
\[ D_ t^{T} = \hat{\alpha }_{t}- \hat{\alpha }_{T} \]
\[ \mr{Intercept }= \hat{\gamma }_{N} + \hat{\alpha }_{T} \]

The sum of squared errors is

\[ \mr{SSE}= \sum _\mi {i = 1} ^\mi {N} \sum _\mi {t = 1} ^\mi {T_\mi {i}} (y_\mi {it} - \gamma _\mi {i}-\alpha _\mi {t} - \mb{X} _{s}\tilde{{\beta }}_{s})^{2} \]

The estimated error variance is

\[ \hat{{\sigma }}_{{\epsilon }}^{2}= \mr{SSE }/ (\mi{M}-\mi{N}-\mi{T}-(\mi{K} -1)) \]

With or without a constant, the covariance matrix of 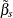${\tilde{\beta }}_{s}$ is given by

\[ \mr{Var}\left[{\tilde{\beta }}_{s}\right] = \hat{{\sigma }}_{{\epsilon }}^{2}(\tilde{\mb{X} }^{'}_{s} \tilde{\mb{X} }_{s})^{-1} \]

For information about the covariance matrix that is related to dummy variables, see the section Two-Way Fixed-Effects Model.