The HPPANEL Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Specifying the Input DataSpecifying the Regression ModelSpecifying the Number of Nodes and Number of ThreadsUnbalanced DataOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsOne-Way Random-Effects ModelTwo-Way Random-Effects ModelBetween EstimatorsPooled EstimatorLinear Hypothesis TestingSpecification TestsOUTPUT OUT= Data SetOUTEST= Data SetPrinted OutputODS Table Names
Specifying the Input DataSpecifying the Regression ModelSpecifying the Number of Nodes and Number of ThreadsUnbalanced DataOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsOne-Way Random-Effects ModelTwo-Way Random-Effects ModelBetween EstimatorsPooled EstimatorLinear Hypothesis TestingSpecification TestsOUTPUT OUT= Data SetOUTEST= Data SetPrinted OutputODS Table Names -
Example

- References
Linear Hypothesis Testing
For a linear hypothesis of the form R 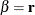 , where
, where 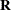 is
is 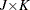 and
and  is
is 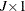 , the F-statistic with
, the F-statistic with 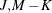 degrees of freedom is computed as
degrees of freedom is computed as
![\[ (\mb{R} {\beta }-\mb{r} )^{'} [\mb{R} \hat{\mb{V} } {\mb{R} ’}]^{-1}(\mb{R} {\beta }-\mb{r} ) \]](images/etsug_hppanel0136.png)
However, it is also possible to write the F statistic as
![\[ F = \frac{(\hat{\mb{u}}^{'}_{*}\hat{\mb{u}}_{*}- \hat{\mb{u}}^{'}\hat{\mb{u}} )/J}{\hat{\mb{u}}^{'}\hat{\mb{u}}/(M - K)} \]](images/etsug_hppanel0137.png)
where
-
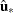 is the residual vector from the restricted regression
is the residual vector from the restricted regression
-
 is the residual vector from the unrestricted regression
is the residual vector from the unrestricted regression
-
J is the number of restrictions
-
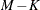 are the degrees of freedom, M is the number of observations, and K is the number of parameters in the model
are the degrees of freedom, M is the number of observations, and K is the number of parameters in the model
The Wald, likelihood ratio (LR), and LaGrange multiplier (LM) tests are all related to the F test. You use this relationship of the F test to the likelihood ratio and LaGrange multiplier tests. The Wald test is calculated from its definition.
The Wald test statistic is
![\[ W=(\mb{R} {\beta }-\mb{r} )^{'}[\mb{R} \hat{\mb{V} }{\mb{R} ’}]^{-1}(\mb{R} {\beta }-\mb{r} ) \]](images/etsug_hppanel0141.png)
The likelihood ratio is
![\[ \mr{LR} = \mi{M} \ln {\left[1 + \frac{1}{\mi{M - K}}JF\right]} \]](images/etsug_hppanel0142.png)
The LaGrange multiplier test statistic is
![\[ \mr{LM} = \mi{M}\left[\frac{\mi{JF}}{\mi{M - K + JF}}\right] \]](images/etsug_hppanel0143.png)
where 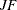 represents the number of restrictions multiplied by the result of the F test.
represents the number of restrictions multiplied by the result of the F test.
The distribution of these test statistics is the 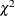 distribution whose degrees of freedom equal the number of restrictions imposed (J). The three tests are asymptotically equivalent, but they have differing small-sample properties. Greene (2000, p. 392) and Davidson and MacKinnon (1993, pp. 456–458) discuss the small-sample properties of these statistics.
distribution whose degrees of freedom equal the number of restrictions imposed (J). The three tests are asymptotically equivalent, but they have differing small-sample properties. Greene (2000, p. 392) and Davidson and MacKinnon (1993, pp. 456–458) discuss the small-sample properties of these statistics.